The Discount Rate Simplified

Posted on December 1, 2012March 26, 2017 By economica

by Christopher Bruce, Laura Weir, Derek Aldridge, and Kelly Rathje

In every personal injury or fatal accident case in which the plaintiff’s loss continues into the future, it is necessary to calculate the rate of interest at which the damages will be invested. This interest rate is commonly called the discount rate, and it is calculated as the nominal (or observed) rate of interest net of the expected rate of price inflation.

As Alberta has no mandated discount rate, the determination of that rate is left to the courts. In this article, we propose to offer a simple technique for identifying this rate.

We proceed in two steps. First, we discuss the criteria that we believe must be met when selecting the discount rate. Second, we apply these criteria to the relevant data, to make that selection. In a separate article following this one, Derek Aldridge and Christopher Bruce contrast the rates that we propose with those that are available on structured settlements.

1. Criteria

The first step in selecting a discount rate is to recognise that the plaintiff is expected to invest his or her award in such a way that the stream of income generated from that award will exactly reflect the stream of losses that the plaintiff has suffered. If the plaintiff has lost $50,000 per year for twenty years, investment of the lump-sum award should produce $50,000 per year, with the principal being exhausted by the end of the twentieth year.

As this stream of investment income is intended to replace a significant portion of the plaintiff’s lifetime earnings, the courts have ruled that the lump-sum should be invested in low-risk financial instruments. Hence:

The discount rate must be based on an investment portfolio that is of low risk.

Although this requirement does not mean that the plaintiff must put all of his or her award into government bonds or guaranteed investment certificates (the lowest-risk investments available), we argue that the interest rate available on those investments provides the most reliable indicator of the rate of return required by the courts.

The plaintiff may well include in his/her portfolio non-government or non-guaranteed investments, such as corporate bonds, mutual funds, and blue chip stocks; but, that the returns on such investments are higher than those obtained from government bonds results primarily from the higher level of risk associated with them – as was seen with devastating results in the post-2008 stock market crash.

The difference between the rate of interest on a government bond or a GIC and, say, a corporate bond is a measure of the compensation that investors demand for accepting a higher degree of risk on the latter investment than on the former. Once that level of “compensation” is deducted, the net, risk-free, interest rate is approximately the same on both. Hence:

The rates of return on Government of Canada bonds and GICs represent reliable indicators of the rate of interest sought by the courts.

Once it has been decided that it is government bond and GIC rates that are to be used, it is necessary to select from among the various options that are available to the plaintiff. Financial advisors recommend that, in order to reduce risk, investors should purchase a mix of bond durations. In that way, if interest rates should rise, investors can sell their short-term bonds and purchase newly-issued bonds at the higher rates; and if interest rates should fall, although investors will have to accept reduced interest rates on any new investments, they will still experience relatively high rates on their long-term (locked-in) investments. Hence:

Plaintiffs should purchase a mix of short-, medium-, and long-term investments.

If the duration of the plaintiff’s loss is less than ten years, the plaintiff will minimize risk by purchasing investments that have durations that mature on the dates on which the losses are incurred. For example, a one-year bond might be purchased to replace the loss one year in the future, a two-year bond to replace the loss two years from now, etc. Hence:

For losses that will occur in the next ten years, the relevant interest rate for any year is the rate of interest on a Government of Canada bond (or GIC) that has a term equal to that number of years.

But if the plaintiff’s loss extends for more than ten years, it will be wise to adopt an investment strategy in which bonds are purchased for shorter terms than the duration of the loss, and then re-invested periodically. To replace a loss twenty years from now, for example, the plaintiff might purchase five-year bonds today and re-invest the returns every five years until the funds were needed. If a similar practice is followed for every duration of loss, the risk that interest rates will rise or fall, relative to what is expected at the time of the initial investment, will be minimised.

Such a strategy, of rolling over short-term investments in order to generate a long-term return, means that the effective discount rate over the term of the investment will be determined not only by the rates that are available today but also by rates that will become available in the future. Thus, the court must predict what those future rates will be.

Contrary to what many experts argue, this prediction can be made simply and with confidence: the most reliable prediction of the rate of interest that will prevail in the long-run is that it will equal the rate of return currently available on long-run bonds. For example, if the current rate on 15-year government bonds is 3.0 percent, the best prediction of the rate of return that will prevail over the next fifteen years is 3.0 percent.

The argument for basing the prediction on this rate can most easily be understood by showing that the contrary cannot be true. For example, it might be argued that “as interest rates are unusually low today, it can be expected that they will eventually rise above current rates.” If this argument is correct, then individuals who wished to invest their funds for long periods of time (for example, individuals who are saving for their retirement) would not purchase long-term bonds today – they would purchase short-term bonds while waiting for interest rates to rise, and then purchase bonds at the new, higher rates once the interest rate had risen.

But if investors behaved this way, the demand for long-term bonds would decrease; and when demand for a bond decreases, its interest rate rises. (Issuers have to raise the rate of return in order to attract investors.) That is, if investors predict that the long-term interest rate will exceed the rate currently available on long-term bonds, they will act in such a way as to drive up the interest rate on long-term bonds. A bond rate that is less than the expected rate cannot be maintained.

Similarly, if investors believed that interest rates were about to fall, they would sell their short-term bonds and purchase long-term. But this would decrease the demand for short-term funds, driving up short-term interest rates, and increase the demand for long-term funds, driving down long-term interest rates.

In short, if the rate of interest that is currently available on long-term bonds is different from the rate that investors expect will prevail in the future, the long-term bond rate will change “towards” the rate that investors predict. As a result, the interest rate available on long-term bonds will always adjust until it equals the rate that investors predict will prevail in the long run. And, as investors have a strong incentive to make correct predictions about the bond market, it is likely that their predictions are the best that are available. Hence, we conclude that:

The best predictor of the rate of interest that will prevail in the long-run is the rate of interest that is currently offered on long-term bonds.

Finally, as we noted in the introduction to this article, the discount rate is found by netting out the forecasted rate of price inflation from the observed nominal rate of interest. Hence, before the discount rate can be determined:

The long-run rate of price inflation must be forecast.

Fortunately, there is a clear consensus that the long-run rate of inflation in Canada will be two percent. This consensus has developed because, since the early 1990s, the Bank of Canada has not only set two percent as its long-run target, it has both met that target and expressed satisfaction with the results of its policy.

That participants in the “money markets” have come to accept that the Bank will achieve this goal over the long-run is seen in two surveys of business leaders that have been conducted annually since 1994. Consistently, respondents have reported that they expect the long-run rate to be 2.0 percent. Indeed, not only has the average, expected rate been 2.0 percent in most years that the surveys were conducted, the variation of responses “around” 2.0 percent has decreased continuously. Hence:

There is a strong consensus that, in the long run, the rate of inflation will average 2.0 percent in Canada. Hence, the discount rate can be found by reducing the forecasted nominal rate by 2.0 percent.

2. Data

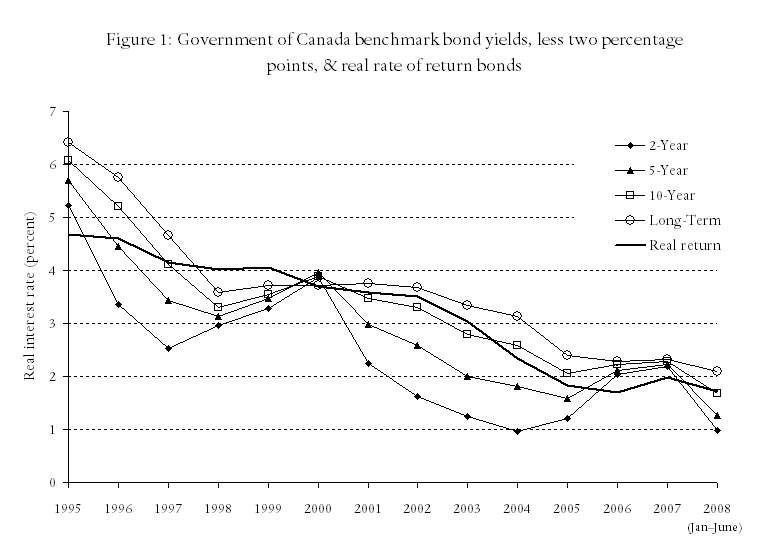
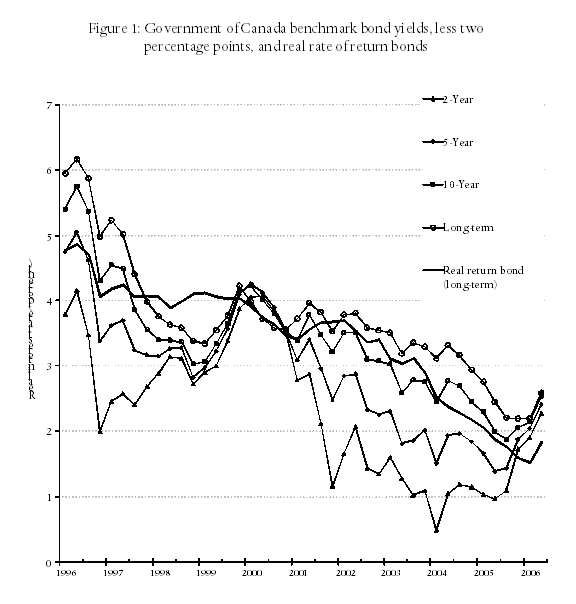
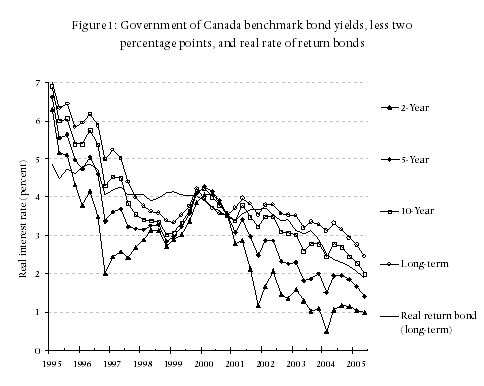
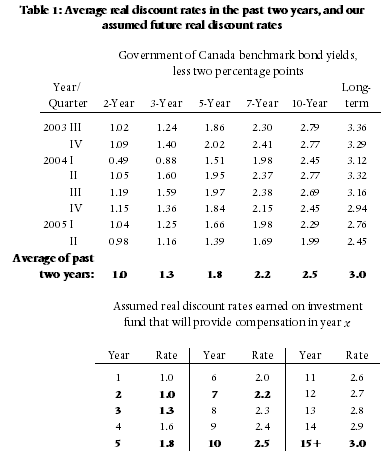
In Figure 1 and Table 1 we report the annual rates of return that have been available since 1995 on five Government of Canada bonds: 2-, 5-, and 10-year bonds, long-term bonds (an average of bonds with a maturity date longer than 10 years), and “real rate of return” bonds (bonds whose rates of return are stated net of inflation). It is seen there that both nominal and real interest rates on Government of Canada bonds have decreased almost continuously since the Bank of Canada introduced its policy of targeting a two percent rate of inflation. Whereas real interest rates were between 4.5 and 7.5 percent in 1995, they have fallen below one percent on most bonds, and even below zero percent on some, in recent years.

What these figures indicate is that investments in government bonds are unlikely to provide real rates of return above zero percent over the next five years; that bonds of five to ten year durations are unlikely to produce rates in excess of 1.0 percent; and that the market expects long-term real interest rates on government bonds to be less than two percent.

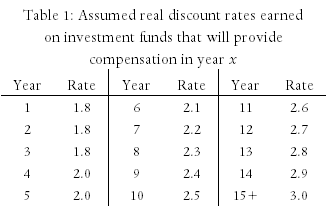
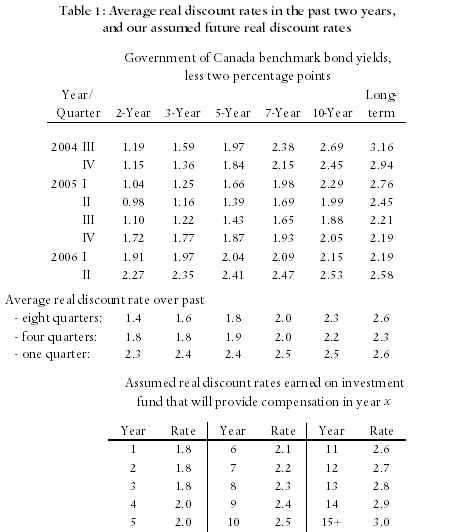
Nevertheless, in recognition of the fact that current rates are at a historical low, we have left our assumed rates at the same values we have employed for the past five years. Those rates, which we report in Table 2, are: 1.8 percent per year on funds invested for three years or less; rising in equal increments to 3.0 percent per year on funds invested for more than fifteen years.

Christopher Bruce is the President of Economica and a Professor of Economics at the University of Calgary. He is also the author of Assessment of Personal Injury Damages (Butterworths, 2004).

Derek Aldridge is a consultant with Economica and has a Master of Arts degree (in economics) from the University of Victoria.

Kelly Rathje is a consultant with Economica and has a Master of Arts degree (in economics) from the University of Calgary.

Laura Weir is a consultant with Economica and has a Bachelor of Arts in economics (with a minor in actuarial science) and a Master of Arts degree from the University of Calgary.

The Discount Rate Revisited (Spring 2008)

Posted on March 1, 2008March 26, 2017 By economica

by Laura Weir, Derek Aldridge, Kelly Rathje, and Christopher Bruce

This article first appeared in the spring 2008 issue of the Expert Witness.

Our readers will recall that every year or two we review our standard discount rate assumptions and publish our findings. It is time to repeat this exercise.

In the Summer 2006 issue of the Expert Witness, we reported that real rates of interest (that is, the rates of return net of inflation) had increased slightly from those outlined in our Summer 2005 article. We responded by increasing our forecast of the short-term (one to six years) real rates of interest. Our forecasted interest rates for the medium to long-term (seven to 15 years or more) remained unchanged – although these rates were slightly higher than the observed real rates of return on Government of Canada bonds, long-term real rate of return bonds, and the long-term rate mandated in Ontario. (Higher rates lead to lower present values, so our estimates can be considered conservative.)

In our 2006 article we specified our assumptions for real interest rates for periods ranging from one-year to 15 years or more. Our assumptions were based on the observed rates of interest on Government of Canada bonds of various terms. We now have more rates to observe and we see that these rates have continued their long-term downward trend. Real rates of interest for five bond series over the last 14 years are depicted in the figure below (with the rates for 2008 estimated using an average of the January through June interest rates).

From the figure we see that real rates have decreased slightly from their 2006 and 2007 levels. However, the decrease in real interest rates is not sufficient to warrant a change in our discount rate assumptions. In particular, we note that the average real rates for the past 12 and 24 months are very similar to the corresponding averages at the time we wrote the previous article. One exception is the long-term rate, whose 24-month average (2.23 percent) is a third of a percent less than the corresponding 24-month average at the time of our previous article.

Although we do not show the comparable interest rates on guaranteed investment certificates (GICs), we have examined them and they are consistently lower than the rates of return on bonds. For example, the rate currently offered for 5-year GICs is approximately three percent, corresponding to a real rate of only one percent.

Our discount rate assumptions, unchanged from our 2006 article, are shown in the table below.

Table 1

Over the years, our approach to forecasting an appropriate discount rate has been criticized by other economists who prefer to rely on historical interest rates in making their forecasts. Below, we address some of these critiques and provide support for our approach.

Our approach, often called the “conservative investment” approach (which assumes a plaintiff will use his damage award to purchase a financial instrument with an appropriate term to maturity and hold that instrument to maturity), has been criticized by other economists who argue for a “market-based” approach (that assumes a plaintiff will buy and sell bonds as interest rates vary instead of holding the bond to maturity). One of us (Bruce) addressed this issue in an article written for the Spring 2007 issue of the Expert Witness entitled “Forecasting the long-term interest rate on Government of Canada bonds: “market-based” versus “conservative” investment“. We summarize his conclusions here as this issue continues to arise.

Some economists suggest that our approach ignores the price changes resulting from changes in the interest rate within the bond market, arguing for the market-based approach that assumes the plaintiff can earn a higher rate of return by actively buying and selling bonds as interest rates change. As a simple example, suppose a plaintiff will incur a loss of income of $100,000, 20 years from now. The conservative approach assumes that he will purchase a 20-year bond, paying five percent in interest per year, for $37,689 and redeem it at maturity for $100,000 to fund his loss in that year.

Assume, however, that the interest rate decreases to four percent one year after purchase. The market-based approach suggests that at four percent, the plaintiff could sell his bond (that has 19 years left to maturity) for $47,464 (= $100,000/1.04¹⁹) and earn $9,775 (= $47,464 – $37,689) in profit, for an effective rate of return of 25.94 percent in one year. However, this is actually not a profit because the plaintiff still has to purchase a 19-year bond (at a cost of $47,464) to fund his $100,000 loss of income 19 years from now. Thus, there is no real benefit to actively trading bonds as the interest rate changes.

In addition to the fact that the effective rates of return under the market-based approach are illusory, effective rates of interest are extremely variable. For example, a publication by the Canadian Institute of Actuaries entitled Report on Canadian Economic Statistics 1924-2005 indicates that the 10-year average (1996-2005) effective real rate of return on long-term Government of Canada bonds was 7.36 percent. However, the standard deviation was 9.01 percent, suggesting an average effective real rate of return that could fluctuate between -1.65 percent and 16.37 percent. This suggests that the plaintiff will almost certainly earn a rate of return different from the average long-term rate. Further, while a “profit” can be made by selling a bond when the interest rate decreases, a “loss” would occur if the interest rate increased (say) to six percent, where the 19-year bond would now only cost $33,051, for a net loss of $4,638 (or an effective rate of return of -12.31 percent).

Finally, if we were to rely on an average of past effective rates of interest then what period should we rely on? For example, the Canadian Institute of Actuaries report noted above indicates that the real effective rate of return on Government of Canada long-term bonds averaged -1.31 percent for the period 1956-1980, +8.74 percent for the period 1981-2005, and +6.79 percent for the period 2001-2005. There would be no justification for relying on any one of the above periods over the others, or for averaging these periods together, in attempting to obtain a forecast of the rate of return in the future.

We use the observed rates on government bonds as an indicator of the rates that are anticipated by large institutional investors, with billions of dollars at stake. While one might find that a forecaster is suggesting that (say) 3½ percent is the appropriate real long-term rate, this prediction is contradicted by the fact that the Government of Canada is presently able to sell its long-term bonds which offer a real return of less than three percent. (If expert institutional investors anticipated that real rates on secure investments will average, say 3½ percent over the next ten years, then they would not buy bonds that pay only 2½ percent, and the Government of Canada would be forced to adjust its bond rates.)

Other economists suggest that it would be simpler to assume that a plaintiff will hold a long-term security and then liquidate portions of this security to fund his/her losses in each year. This is simply another version of the market-based approach and, as discussed, there is a great amount of risk inherent in this strategy. Under our approach, if a plaintiff purchases a 5-year government bond with a value at maturity of $10,000, then in five years he is virtually guaranteed to receive $10,000 after redeeming his bond. However, if he were to buy a 20-year bond with the idea that he would liquidate portions of it to fund losses in each year, then he would be at the mercy of the bond prices available in each year. That is, he would be selling portions of his bond (as opposed to redeeming bonds for the guaranteed maturity value) and so, would be relying on the price of bonds attainable at the date he needed to fund his losses. As our discussion regarding the “conservative” versus “market-based” approaches illustrates, a plaintiff trying to fund his losses during periods of high interest rates would likely be selling portions of his bond at prices lower than his original purchase price and so, may not be able to fund his losses in each future year. If there is pressure on interest rates to increase in the next few years, as many economists feel is the case, then it is likely that plaintiffs investing awards from trials occurring in the next year or two would find themselves in this situation. We do not believe it is reasonable to impose this level of risk on a plaintiff.

Over the last ten years our prediction concerning the long-term interest rate has gradually declined from 4¼ percent to three percent. This decline has been in step with the observed rates, which can be seen in the above chart. Other economists have commented on our changes, with the implication that these changes demonstrate a weakness in our methodology. Our response is that the long-term rate has been changing over the past ten years, and it is important to reflect these changes in our calculations. To do otherwise would result in us using interest rates that are inconsistent with the rates that are actually available to plaintiffs.

Even if one finds that over the past few decades, long-term real interest rates have averaged 3½ percent, that rate is not now available to plaintiffs. Today’s plaintiff seeking secure investments simply cannot obtain a guaranteed long-term rate as high as the rates that were available 10 or 20 years ago. Even if the long-term rate rises to 3½ percent in five years, it does not follow that today’s plaintiff will be able to earn a long-term rate of 3½ percent, since he will be limited to the lower rates for the first five years.

Finally, many economists argue that plaintiffs should invest in equities, as well as bonds, and argue that this would result in a portfolio that is less volatile than investing in bonds alone. We find it difficult to justify the assertion that a portfolio that includes equities would be less volatile, given that the value at maturity of Government of Canada bonds is virtually guaranteed. Remember, the purpose behind the plaintiff’s investment of an award is to fund his losses in each future year and this is much different from investing for (say) retirement. The plaintiff must be able to fund his future losses in each year, whereas retirement can be delayed (or retirement plans changed) if there are insufficient funds. A plaintiff who invests in a series of bonds that provide the amount needed to fund his loss in each year, will receive the necessary amount with little to no risk of default. The same can not be said of equities, which carry a very real risk of default. The inclusion of equities can only increase the risk that a plaintiff will not be able to fund their future losses in each year.

We will re-examine our assumptions next year, and expect that some minor adjustments in our shorter-term rates may be warranted, depending on the movement of rates between now and then. As noted, minor changes in our assumptions regarding short-term interest rates will typically lead to negligible changes to our present value estimates. The assumed longer-term rates have a greater influence on our calculations, and if the rate on long-term bonds remains significantly below three percent (as it has since 2004), it may be appropriate to adjust our long-term rates as well.

Laura Weir, Derek Aldridge, Kelly Rathje, and Christopher Bruce are consultants with Economica.

Forecasting the long-term interest rate on Government of Canada bonds: “market-based” versus “conservative” investment

Posted on March 1, 2007March 26, 2017 By economica

by Christopher Bruce

This article first appeared in the spring 2007 issue of the Expert Witness.

Introduction

In order to calculate the lump-sum, or discounted, value of a future stream of earnings, the financial expert must forecast the rate of interest (or discount rate) at which the plaintiff’s damages will be invested. Although most experts now base this forecast, to a large extent, on the rates of interest available on Government of Canada bonds, disputes have arisen concerning the manner in which the data concerning these bonds should be interpreted.

Fundamentally, the question comes down to one of whether the plaintiff can be assumed to take a “conservative” approach, in which she invests her damages in long-term bonds and holds those bonds to maturity; or whether she can be assumed to follow a “market-based” (or “speculative”) approach in which she buys and sells bonds as market conditions change.

Whereas Economica favours what I have called the conservative approach, some other economists employ the market-based approach. In this article, I first describe how interest rates are determined under each of these approaches and then I explain why I believe that the market-based approach is inappropriate.

Definitions

Imagine the following scenario: the court has ruled (i) that one component of the plaintiff’s damages is a loss of $50,000 twenty years from now; and (ii) that the interest rate to be used to discount this loss is five percent. In this case, the lump sum value of the loss can be determined to be $18,844 (= $50,000/1.05²⁰).

It is possible that the court could have obtained its interest rate assumption simply by observing the rates offered on twenty-year bonds – what I will call the “posted” rates. Implicitly, in that case, it would have been assuming that the plaintiff will use his damages to purchase a twenty-year bond (or similar, long-term financial instrument) that pays five percent per annum; and that he will hold that bond until maturity. I call this the “conservative” approach.

Alternatively, however, the court might have assumed that the plaintiff will not hold his bond until maturity, but will buy and sell bonds as interest rates vary. In this approach, the effective interest rate will be the average of the rates that the plaintiff can expect to earn over the twenty year period. I call this approach the “market-based investment” approach.

Market-based investment in bonds operates in the following way: Imagine that, at a time when posted interest rates are five percent, the plaintiff has paid $18,844 to purchase a twenty-year bond worth $50,000 on maturity. Assume also that, one year later, interest rates have fallen to four percent. At that rate, it would cost $23,732 (= $50,000/1.04¹⁹) to purchase a bond that paid $50,000 nineteen years in the future. The plaintiff could now sell his twenty-year bond, (which, after a year, has nineteen years left on it), for this amount – making a profit of $4,888 (= $23,732 – $18,844), or an effective rate of return of 25.94 percent, in one year.

Rates such as this can be earned on long-term bonds as long as the interest rates on those bonds are falling. For example, a bond that pays $10,000 ten years from now will cost $5,584 when interest rates are six percent; and a bond that pays $10,000 nine years from now will cost $6,446 when interest rates are five percent. Thus, the investor who purchases a ten-year bond at six percent will be able to sell it one year from now for a profit of $862 (= $6,446 – $5,584), or an effective return of 15.44 percent (= $862/$5,584), if interest rates fall to five percent.

Whenever interest rates are falling, the investor who actively trades long-term bonds will make effective rates of return that exceed the rates that would be obtained if those bonds were held to maturity.

Conversely, however, if interest rates are rising, the market-based trader will earn effective rates that are lower than the posted rates. For example, if the interest rate is seven percent, a bond that pays $10,000 nine years from now will cost $5,439 (= $10,000/1.07⁹). It was seen above, however, that a bond that pays $10,000 ten years in the future will cost $5,584 when interest rates are six percent. Thus, an investor who purchases a ten-year bond at six percent will lose $145 (= $5,439 – $5,584), for an effective “return” of -2.6 percent, if interest rates fall to seven percent and he sells it one year later.

What is less clear from these examples is that, if the effective interest rates are averaged over a long period of time, they will equal the rates that investors would have obtained had they held their bonds to maturity. Over the long-run, the investor who sells multi-year bonds after one year, and replaces them each time with other multi-year bonds, will average the same rate of return as an investor who buys and holds bonds to maturity.

Data

Table 1 reports both the posted and the effective rates of interest on Government of Canada bonds of 10+ years to maturity, for the last 25 years. It is seen in the first column of this table that posted interest rates have fallen almost continuously over the entire period: from 15.22 percent in 1981 to 4.39 percent in 2005.

Table 1

Given the discussion above, therefore, we expect to see that effective interest rates over most of this period would exceed the posted rates. It is seen in the second column of Table 1 that this is what happened. Particularly noticeable is the effective rate in 2005: 15.05 percent at a time when posted rates were in the four to five percent range.

As those who argue for the use of effective rates anticipate that the average of those rates will equal the average of the posted rates over the long run, Table 2 reports average posted and effective rates, both in nominal and “real” terms, for various sub-periods in the last 50 years.

Table 2

It is seen there that, whether nominal or real (i.e. net of inflation) rates are used, effective rates have exceeded posted rates in every sub-period in the last 25 years. For example, whereas the average effective nominal rate was 12.49 percent between 1981 and 2005, the average posted rate was 8.64 percent. The comparable real rates were 8.74 and 5.00 percent, respectively, a difference of over three percentage points in each case.

Only if a fifty year period is used do the effective and posted rates begin to approach one another – primarily because the 25 year period from 1956 to 1980 experienced extremely low effective rates of return (hence balancing the high rates from 1981-2005 in the calculation of the fifty-year average).

Drawbacks to Use of the Effective Rate

A review of the information contained in Tables 1 and 2 makes it clear that there are many disadvantages to the use of the effective rate as an indicator of the rate of return that plaintiffs will be able to obtain in the future.

1. The most serious difficulty with this rate is that it has been extremely variable. As a result, one can obtain almost any estimate of the real effective rate that one wishes, simply by choosing the appropriate time period.

Those who wish to argue for a very high rate might choose the fifteen-year period 1991-2005, with an average rate of 9.39 percent, for example. Whereas those who wish to argue for a much lower rate could choose the fifty-year period 1956-2005, with an average rate of 3.71 percent – or even the 60-year period 1946-2005, with an average of 2.44 percent.

There is no sound reason for choosing any one of these periods over the other. For example, it would be difficult to justify averaging together the 1956-1980 average, of -1.31 percent, with the 1981-2005 average, of 8.74 percent, to obtain a forecast of the rate of return obtainable over the next ten years.

2. A related problem is that the extreme variability of the effective rate virtually guarantees that the rate of return the investor will actually earn will differ significantly from the average rate obtainable over the long run. Hence, it would never be prudent to advise plaintiffs to adopt the market-based investment approach on which the effective rate is based.

3. Because long-term interest rates have been falling for 25 years, they have reached levels so low that most analysts believe they will not fall further – they certainly cannot fall by more than ten percentage points, as they did between 1981 (15.22 percent) and 2005 (4.39 percent). This means that the very high effective rates that have been observed in the last 25 years will not be observed again. Indeed, it is highly likely that nominal rates will rise over the near future, causing effective rates to fall, perhaps even into negative figures. As a result, plaintiffs would not be well-advised to engage in market-based investment in bonds.

4. Even if effective rates are positive, and above posted rates, the effective rate is not an appropriate rate for determining long-term rates of return on investments.

Return to the example developed in the first section of this article: The court has found that the plaintiff will lose $50,000 twenty years from now. Hence, if the interest rate is five percent, the lump-sum value of the plaintiff’s damages amount to $18,844. If, between now and one year from now, the interest rate falls to four percent, the plaintiff will be able to sell his bond for $23,732, earning a one-year rate of return of 25.94 percent.

But the plaintiff still needs to set aside enough money to replace his future $50,000 loss. At the new four percent interest rate, this will cost him $23,732. The money he has “earned” by selling his bond now has to be spent to replace it. Thus, the high effective rate of interest is illusory.

Christopher Bruce is the President of Economica and a Professor of Economics at the University of Calgary. He is also the author of Assessment of Personal Injury Damages (Butterworths, 2004).

The Discount Rate Revisited (Summer 2006)

Posted on June 1, 2006March 26, 2017 By economica

by Derek Aldridge

This article first appeared in the summer 2006 issue of the Expert Witness.

Our readers will recall that every year or two we review our standard discount rate assumption and publish our findings. It is time to repeat this exercise.

One year ago, in the Summer 2005 issue of the Expert Witness, we reported that real rates of interest (that is, the rate of return net of inflation) had continued their downward trend. We responded by lowering our forecast of the long-term real rate of interest to three percent – a rate that was slightly higher than the observed real rate of return on long-term Government of Canada bonds, long-term real rate of return bonds, and the long-term rate mandated in Ontario. (Higher rates lead to lower present values, so our estimates can be considered conservative.)

In addition, we made a change to how we applied our discount rate assumptions in our calculations. Previously we had assumed that the plaintiff’s entire lump sum award would earn a given interest rate, regardless of the fact that part of the award might be needed to fund next year’s losses and another part might be needed to fund losses 20 years from now. Our revised approach was to assume that the plaintiff will invest part of his award in short-term investments, part in medium-term investments, part in long-term investments, and so forth. This more accurately reflects the behaviour that would be expected from a plaintiff, and it more accurately reflects the different returns he can expect from his short-term investments versus his long-term investments. [*]

In our previous article we specified our assumptions for real interest rates for periods ranging from one-year to investments of 15 years or more. Our assumptions were based on the observed rates of interest on Government of Canada bonds of various terms. We now have four more quarters of rates to observe and we see that, except for the returns on long-term bonds, rates have increased. The trend in real rates over the last ten years is depicted in the chart below.

Note that to determine the real interest rate we deduct two percentage points from the “nominal” or observed interest rates to reflect inflation anticipated by investors. As the Bank of Canada has managed to keep the core rate of inflation within a small band around this target since the early 1990s, and as it has been the stated intention of not only the Bank of Canada but most other central banks (most notably that of the European Union) to keep the inflation rate at that level, there is now virtual unanimity among investors that two percent will be the long run rate of inflation in Canada. Accordingly, it can be concluded that investors have been acting as if the real rate of interest is the observed, nominal rate less two percent.

From the chart we see that most real rates began to rise with the third quarter of 2005. Long-term government bonds did not begin their rise until the second quarter of 2006 and are now only slightly higher than they were a year ago. The pattern has been similar for real rate of return bonds. Given these changes, we believe a slight increase in our shorter-term rates is warranted, though we will not change our longer-term rates. The most recent two years of real rates are shown in the table below, along with the rates that we will use in our calculations.

Table 1

The change from the rates we have been using for the past year is very modest. Only the rates for years 1-6 have changed at all, and these changes will have a negligible impact on our calculations. The present value of losses that will end within five years will decrease by about one percent relative to our previous assumption, while losses that extend for more than five years will fall by an even smaller amount.

Note that we are not specifically assuming that plaintiffs will invest their awards in government bonds and hold them to maturity. There are a variety of reasonable investment strategies they could pursue. We use the observed rates on government bonds as an indicator of the rates that are anticipated by large institutional investors, with billions of dollars at stake. While one might find that a forecaster is suggesting that (say) 3½ percent is the appropriate real long-term rate, this prediction is contradicted by the fact that the Government of Canada is presently able to sell its long-term bonds which offer a real return of less than three percent. (If expert institutional investors anticipated that real rates on secure investments will average, say 3½ percent over the next ten years, then they would not buy bonds that pay only 2½ percent, and the Government of Canada would be forced to adjust its bond rates.)

Over the last ten years our assumption regarding the long-term interest rate has gradually declined from 4¼ percent to three percent. This decline has been in step with the observed rates, which can be seen in the above chart. Other economists have commented on our changes, with the implication that these changes demonstrate a weakness in our methodology. Our response is that the long-term rate has been changing over the past ten years, and it is important to reflect these changes in our calculations. To do otherwise would result in us using interest rates that are inconsistent with the rates that are actually available to plaintiffs.

Even if one finds that over the past few decades, long-term real interest rates have averaged 3½ percent, that rate is not now available to plaintiffs. Today’s plaintiff seeking secure investments simply cannot obtain a guaranteed long-term rate as high as the rates that were available 10 or 20 years ago. Even if the long-term rate rises to 3½ percent in five years, it does not follow that today’s plaintiff will be able to earn a long-term rate of 3½ percent, since he will be limited to the lower rates for the first five years.

As noted, we have changed our assumptions regarding the shorter-term discount rates, but not the longer-term rates. We expect that our estimates of the long-term rate discount rate will change less frequently and to a lesser extent than our estimates of the shorter term rates. This simply reflects that shorter-term rates are inherently more volatile than long-term rates. This can be seen in these charts (Figure 2), which show the percentage point changes in the quarterly real interest rates over the last ten years.

Footnotes

* To illustrate the effect of this approach, note that a child plaintiff who will not experience a loss of income for ten years will manage to earn a relatively high rate of return because he will be able to invest in “long-term” investments, and he will be more likely to benefit from possible future increases in interest rates. On the other hand, an older plaintiff who will experience a loss of income over the next five years only, will not be able to benefit from long-term investments or from possible increases in interest rates. She will face the low rates available on short-term investments. [back to text of article]

Derek Aldridge is a consultant with Economica and has a Master of Arts degree (in economics) from the University of Victoria.

The Discount Rate Revisited

Posted on June 1, 2005March 24, 2017 By economica

by Christopher Bruce, Derek Aldridge, Kelly Rathje, and Hugh Finnigan

This article first appeared in the summer 2005 issue of the Expert Witness.

In the Autumn 2000 issue of this newsletter, we conducted an extensive review of the various methods of measuring the real rate of interest, or discount rate, and presented evidence concerning the movement of those measures over the period 1995-2000. (That article is available on our website, at economica.ca/ew53p1.htm.)

That survey was subsequently updated in our Winter 2001/02 and Spring 2003 issues. What we found in both of those updates was that interest rates had begun to fall relative to the historically high levels that had persisted over most of the 1990s.

At the time of our Spring 2003 article, we concluded that the best estimate of the long-run discount rate was 3¼ percent. But we also argued that, as interest rates on short-term bonds and GICs were lower than those on longer term investments, it would be appropriate to employ an interest rate of 2¼ percent on the first five years of any investment.

The primary purpose of this article is to examine nine additional quarters (27 months) of data to determine whether the trend we observed in our earlier articles has continued, or whether a revision in our recommended interest rate is appropriate. We also report on recent changes to Ontario’s mandated discount rate; and we revisit the question of whether forecasts of future interest rates should be based on information about past interest rates or on information about current, long-run interest rates.

Revised Data

Instead of providing tables of data comparable to those presented in our earlier articles, we now present a chart that shows the trend in interest rates since 1995. The complete data set can be found on our web site (see www.economica.ca/ew102p1.htm). Figure 1 shows the trend in real interest rates on government bonds of various term lengths, as well as the rate of return on real rate of return bonds.

Note: We deduct two percentage points from the “nominal” or observed interest rates to reflect inflation anticipated by investors. As the Bank of Canada has managed to keep the core rate of inflation within a small band around this target since the early 1990s, and as it has been the stated intention of not only the Bank of Canada but most other central banks (most notably that of the European Union) to keep the inflation rate at that level, there is now virtual unanimity among investors that two percent will be the long run rate of inflation in Canada. Accordingly, it can be concluded that investors have been acting as if the real rate of interest is the observed, nominal rate less two percent.

The data in Figure 1 indicate that real rates of interest have continued the downward trend that began in 1996/97. Whereas we concluded two years ago that long-term real interest rates were approximately 3¼ percent and short-term rates approximately 2¼ percent; it now appears that real rates have fallen substantially below those levels. In particular, note that the rate of return on 10-year Government of Canada bonds, net of the 2 percent expected rate of inflation, is now below 2 percent and has not exceeded 3¼ percent (our earlier prediction of the “long-term” rate) since early 2002. Even the real rate on long-term (30-year) Government of Canada bonds has fallen below 2½ percent in the most recent quarter. And the rate of return on real rate of return bonds is now below 2 percent and has not been above 3 percent since mid-2003.

Although we do not show the comparable interest rates on guaranteed investment certificates (GICs), we have examined them and they are consistently lower that the rates of return on bonds. For example, the real rates on 1-year GICs have been consistently negative since late-2001, meaning that investments in one-year GICs are not keeping pace with inflation. The real rate on 5-year GICs has been below one percent for all but two of the last eight quarters and has not exceeded two percent since early 2002.

Forecasting the Real Rate of Interest

For some time now, Economica has been arguing that current interest rates, net of the two percent expected rate of inflation, provide the most reliable basis on which to predict future interest rates. Some other economic experts in Western Canada disagree with us, and base their forecasts on information about historical interest rates. We consider their position to be unjustified. We explain why here:

The continued dramatic fall in interest rates.

First, as a glance at Figure 1 will indicate, the real rate of interest in the last decade has fallen continuously and dramatically: the long-term rate has fallen from about 7 percent to below 2½, while the short-term rate has fallen from about 6 percent to below 1 percent. Clearly, any prediction that was based on an average of the figures in this period (or any other period extending back to the early 1980s) would seriously overstate the rates that will be available to a plaintiff investing his or her award today.

It is important to note that although rates are low by historic standards, today’s investors who seek the security of investments comparable to government bonds and GICs cannot avoid these low rates. The fact that average interest rates over the last 30 years were much higher does not help today’s plaintiff-investor. Even if one believed that long-term real rates will rebound to (say) 3.5 percent in the next 5-10 years, the best that today’s investor will be able to do is place his funds in 5-10 year investments earning 1.5-2 percent and then hopefully reinvest at the higher 3.5 percent rate. This of course will not yield nearly the same result as if he had been able to invest at 3.5 percent right from the start.

Economic theory.

Second, the fall in real interest rates is consistent with macroeconomic theory. Specifically, many macroeconomists are arguing that the relatively high real interest rates that were observed in the 1980s resulted from the high volatility in expectations concerning the nominal rate of inflation. That is, when inflation is unpredictable, investors who place their funds in long-term bonds face a considerable amount of uncertainty. If inflation proves to be higher than expected, the real rate of return that they realise may be very low or even negative. To compensate for this uncertainty, investors demand a relatively high expected rate of return. Conversely, when inflation becomes predictable, as has happened in the last five to ten years, investors face much less uncertainty and are willing to accept lower real rates of return. Accordingly, there is sound reason to believe that, as long as the Bank of Canada maintains its current course[*] (which it is expected to do), both nominal inflation and real interest rates will remain at the low levels that have been observed recently.

Furthermore, most economists believe that real interest rates will be higher in a period in which governments run large deficits – and, therefore, have to borrow heavily – than in those in which revenues exceed expenditures. As is well known, although the Canadian government ran sizeable deficits in the late 1980s and 1990s, it has now adopted a goal of achieving a balanced (or, even, surplus) budget. Again, this leads us to believe that real interest rates will be lower in the future than they were in the 1980s and 1990s.

The actions of large, institutional investors.

Most of the bonds reported in Figure 1 are purchased by large, institutional investors, such as pension funds. That these investors are willing to purchase, say, ten-year bonds paying a real rate of approximately two percent, or real rate of return bonds that are paying below two percent (as of the second quarter of 2005) indicates that they do not anticipate that they can obtain better rates of return on other secure investments. That is, regardless of whether private investors actually purchase the government bonds identified in Figure 1, the returns on those bonds indicate that the institutions that base millions of dollars of investment on their predictions of the financial markets are forecasting that real rates of return will remain low in the foreseeable future. (If expert institutional investors anticipated that rates on secure investments will average, say 3½ percent over the next ten years, then they would not buy bonds that pay only two percent, and the Government of Canada would be forced to adjust its bond rates.)

A future increase in rates will have little effect on most plaintiffs.

Even if real interest rates were to increase substantially in the next ten years or so, (against expectations), that would have relatively little effect on the investments of many plaintiffs, for two reasons. First, it is the rates of return that are available today that will dictate the average rate that plaintiffs will be able to obtain over at least the first 5-10 years of the period of their loss. As noted above, if rates increase in the future, the best that today’s plaintiff can do is place his funds in 5-10 year investments at today’s low rates and then later reinvest at the (hopefully) higher future rates. Even if rates return to their historical average, this investment approach will still yield an average rate of return that is below the historical average. Second, since most plaintiffs will need to begin consuming their award immediately (to replace their lost income and fund their costs of care), the most substantial portion of the interest that they will earn on the investment of their awards will occur in the first half of their period of loss, before they have drawn down much of their capital (that is, during the period in which they are funding most of their annual losses from interest income). If the period of loss is 20 years or less (like most plaintiffs), then the interest they earn in the first ten years will have a much greater impact on their investments than the interest they earn in the next ten years. Thus a return to higher interest rates after 10 years or so will have only a small impact on these plaintiffs. For plaintiffs with a period of loss that is only ten years or less, future increases in interest rates will have almost no effect on their investments.

Note that one implication of relying heavily on current interest rates is that it requires that we change our discount rate assumption more frequently than if we simply relied on historical averages. However, making changes to our discount rate assumption does not imply a weakness in our methodology. To do otherwise would result in us using interest rates that we know are inconsistent with the rates that are actually available to plaintiffs. Even if one believed that over the long-term, real interest rates will average (say) 3 or 3½ percent, it does not necessarily follow that our discount rate assumptions should remain fixed. This is because (as we explained above), the rates of return over the next ten or so years will have a substantial impact on the investment results of most plaintiffs. Thus, it is important to account for the rates that are available to plaintiffs now, as well as the rates that will be available (on average) over the long-term.

Ontario’s mandated discount rate

Following a detailed review, Ontario (in year 2000) revised its regulations concerning its mandated discount rate. The new methodology that was chosen yields a discount rate of 1.5 percent for the first fifteen years of any award and 2.5 percent for all years beyond that point. Specifically, Ontario’s revised regulation 53.09 states:

53.09 (1) The discount rate to be used in determining the amount of an award in respect of future pecuniary damages, to the extent that it reflects the difference between estimated investment and price inflation rates, is,

(a) for the 15-year period that follows the start of the trial, the average of the value for the last Wednesday in each month of the real rate of interest on long-term Government of Canada real return bonds (Series V121808, formerly Series B113911), as published in the Bank of Canada Weekly Financial Statistics for the 12 months ending on August 31 in the year before the year in which the trial begins, less 1 per cent and rounded to the nearest ¼ per cent; and

(b) for any later period covered by the award, 2.5 per cent per year. O. Reg. 488/99, s. 2; O. Reg. 263/03, s. 4 (1).

The average month-end rate of return on real rate of interest bonds from September 2003 through August 2004 was 2.58 percent. Deducting one percentage point and rounding to the nearest quarter percent yields a mandated discount rate of 1.5 percent for trials that occur in 2005. Given the rates on real rate of interest bonds since September 2005, we can also be almost certain that Ontario’s mandated discount rate (for the first 15 years of loss) will fall to 1.0 percent for trials that occur in 2006.

As discussed in an earlier article (see “Ontario’s Mandated Discount Rate – Rule 53.09(1)” that appeared in the Autumn 2000 issue of the Expert Witness), we have a concern with Ontario’s policy of deducting one percentage point from the one-year average of the rate on real rate of return bonds. What is perhaps more interesting is their finding that 2.5 percent reflects the long-term real rate of interest. This rate is lower than the long-term rate we have been using, though it is consistent with the current rate on long-term Government of Canada bonds.

Conclusion

Our review of the empirical and theoretical sources suggests that it would be appropriate to adjust our discount rate assumption. We also propose to make a change in how we apply our discount rate assumptions in our calculations. Whereas we previously assumed that the real rate of return on all of a plaintiff’s investments would be 2.25 percent for the first five years and 3.25 percent thereafter, we now assume that for income required in the first few years, an investment will be made at short-term rates, while for income needed in the more distant future, investments will be made that will earn the predicted long-term rates. Below we will further explain the approach we will use for our calculations, and then we will outline the discount rate assumptions we will use.

To illustrate the effect of this approach, note that a child plaintiff who will not experience a loss of income for ten years will manage to earn a relatively high rate of return because he will be able to invest in “long-term” investments, and he will be more likely to benefit from possible future increases in interest rates. On the other hand, an older plaintiff who will experience a loss of income over the next five years only, will not be able to benefit from long-term investments or from possible increases in interest rates. She will face the low rates available on short-term investments.

Consider the following example of a plaintiff who will incur a loss of income of $10,000 seven years from now. If she is compensated for the future loss today, she could use her award to purchase a government bond with a seven-year term, and not touch the award until it is needed in seven years, when the bond matures. We will see in Table 1 (below) that such a bond has been paying about 2.2 percent, net of inflation over the last two years. This plaintiff will not need to invest at the lower rates offered by shorter-term assets, but she will also not benefit from the rates offered on longer-term bonds, nor will she benefit from a possible future increase in interest rates. To invest her award in secure assets she faces two options: she can make successive short-term investments in hopes that the rates will increase in the near future, or she can make a longer-term (seven-year) investment and accept the interest rate that is available to her. Given her investment-obligations as a plaintiff, we would expect that that latter option would be more appropriate. Even if she chose the former option we would not expect her overall return to improve, unless we knew that rates would increase in the near future. (And if it was known that rates will increase in the near future, then this increase would already be reflected in the current rate of return offered on seven-year bonds.)

For our calculations we will choose an average rate of return that will be earned on investments that are held until each future year of the period of loss. For example, we assume that the portion of the plaintiff’s award that is held for seven years to compensate her for her loss in year 7 will earn an average rate of return of 2.2 percent. Similarly, we assume that the portion of the plaintiff’s award that is held for 15 years to compensate her for her loss in year 15 will earn an average rate of return of 3.0 percent. And so forth.

To obtain the discount rates for use in our calculations, we propose to take an average of the most recent two years of quarterly interest rates (using two years of monthly rates would yield the same results), for the Government of Canada benchmark bond yields for 2-, 3-, 5-, 7-, 10-year, and long-term bonds. After deducting two percentage points for anticipated inflation and rounding to the nearest tenth of a percent, this will give us our assumed real interest rates for various future terms. We assume the one-year rate is the same as the reported two-year rate, and for the “in-between” years we simply extrapolate. We assume that the long-term rate applies to year 15 and beyond. The rates that result from this approach are shown in Table 1.

Table 1

Note that we believe that the rates proposed in Table 1 (above) remain conservative (that is, they may understate future losses) since they reflect interest rates that have been available over the past two years, instead of only the rates that are available now (even though only the rates available now can be assured to today’s investor).

Footnotes

* Since approximately December 1993, the Bank of Canada has successfully maintained a policy of keeping inflation at a two percent target (the midpoint of its 1-3 percent target range). [back to text of article]

Christopher Bruce is the President of Economica and a Professor of Economics at the University of Calgary. He is also the author of Assessment of Personal Injury Damages (Butterworths, 2004).

Derek Aldridge is a consultant with Economica and has a Master of Arts degree (in economics) from the University of Victoria.

Kelly Rathje is a consultant with Economica and has a Master of Arts degree (in economics) from the University of Calgary.

From 2003 through 2005, Hugh Finnigan was a consulting economist at Economica, with a Master of Arts degree from the University of Calgary.

Selecting the Discount Rate – An Update

Posted on March 1, 2003March 24, 2017 By economica

by Christopher Bruce, Derek Aldridge, Kelly Rathje, and Scott Beesley

This article first appeared in the spring 2003 issue of the Expert Witness.

That survey was subsequently updated in our Winter 2001/2002 issue (Vol. 6, No. 4). What we found was that interest rates had begun to fall, relative to the historically high levels that had persisted over most of the 1990s.

At that time, we concluded that the best estimate of the long-run discount rate was 3½ percent. But we also argued that, as interest rates on short-term bonds and GICs were lower than those on longer term investments, it would be appropriate to employ an interest rate of 2½ percent on the first five years of any investment.

The purpose of this article will be to provide five additional quarters (15 months) of data to determine whether the trend we observed at the beginning of 2002 has continued, or whether a revision in our recommended interest rate is appropriate.

Revised data

Tables 1 and 2 provide updates of the information contained in the equivalent tables of the Winter 2001/2002 article. In particular, we have added data for all four quarters of 2002 plus the first quarter of 2003.

Table 1 reports the “raw” data from which some of the real interest rate figures in Table 2 have been calculated. The first column reports the “core rate of inflation” – a measure of the rate of inflation that removes the effects of change in those components of the price index that often move erratically, such as food, energy, and taxes. It is often argued that this measure offers a more reliable predictor of future changes in prices than does the “standard” measure of price inflation. (See the Autumn 2000 article for a detailed description of the core rate of inflation.)

The next three columns in Table 1 report the rates of return on Government of Canada 5-year and 10-year bonds and on 5-year Guaranteed Investment Certificates (GICs). The former represent the minimum rates of return that investors can expect on safe investments. The rate of return on GICs, on the other hand, represents the interest rate available on a mixed, low-risk portfolio of stocks and bonds.

Table 1

Table 2 reports seven measures of the real rate of interest – that is, the rate of interest net of the expected rate of inflation. The first of these is the market-determined rate of return on “real rate of return bonds” – bonds whose value is denominated in terms of the real rate of interest. These bonds are of particular importance because they are purchased by sophisticated investors and because they tend to held for long periods of time.

The second, fourth, and sixth columns report the 5- and 10-year government bond interest rates and 5-year GIC rates net of the core inflation measure.

Finally, columns three, five, and seven report the government bond and GIC rates net of the Bank of Canada’s target rate of inflation of 2 percent. As the Bank has managed to keep the core rate of inflation within a small band around this target for the last eight years, it is widely believed that 2 percent is the rate that is expected by most investors. That is, investors are believed to act as if the real rate of interest is the observed, nominal rate less 2 percent.

Table 2

Interpretation of the data

The data in Table 2 indicate that real rates of interest have continued the downward trend that began in 1996/1997. Whereas we concluded a year ago that long-term interest rates were approximately 3½ percent and short-term rates approximately 2½ percent; it appears that those rates have now fallen to 3 percent and 2¼ percent, respectively.

Note that the latter rate is close to the rates reported in the Bank of Canada’s Monetary Policy Report of April 2003 (Chart 19, p. 24).

In addition, 3 percent is the rate at which the Bank of Canada recently issued a new set of 33-year real rate of interest bonds. As we argued in the Autumn 2000 issue of the Expert Witness, the rate of return on these bonds is a particularly reliable estimate of the expected real interest rate as they are purchased primarily by large institutional investors (like pension funds) that have made considerable investments in the prediction of future rates of interest and inflation.

For this reason, we believe that it would be appropriate to revise our existing 2½ and 3½ percent two-part forecast of real interest rates. Based primarily on the observed rate on 5-year Government of Canada bonds, we propose to use a rate of 2¼ percent for the first five years of all calculations. For all subsequent years we propose to use a rate of 3¼ percent – though we note that a rate as low as 3 percent could be supported based on the most recent observed rates on 10-year Government of Canada bonds and based on the Bank of Canada’s current issue of real rate of return bonds. Our long-term rate is perhaps slightly conservative, but we will re-examine this issue next year and decide then if changes are warranted.

Christopher Bruce is the President of Economica and a Professor of Economics at the University of Calgary. He is also the author of Assessment of Personal Injury Damages (Butterworths, 2004).

Derek Aldridge is a consultant with Economica and has a Master of Arts degree (in economics) from the University of Victoria.

Scott Beesley is a consultant with Economica and has a Master of Arts degree (in economics) from the University of British Columbia.

Kelly Rathje is a consultant with Economica and has a Master of Arts degree (in economics) from the University of Calgary.

Selecting the Discount Rate – An Update

Posted on December 1, 2001March 24, 2017 By economica

by Christopher Bruce, Derek Aldridge, Scott Beesley, and Kelly Rathje

This article was originally published in the Winter 2001/02 issue of the Expert Witness.

At that time, we concluded that our best estimate of the long-run discount rate was 4.0 percent. But we added the caveat that, as interest rates in 2000 had deviated significantly from the average of the preceding years, it would be important to maintain a close watch on those rates – to determine whether 2000 was an aberration or whether it represented the beginning of a new trend.

In particular, we concluded that article with the statement:

If bond rates do not rise relative to the rate of inflation in the near future, we will be revising our real rate of interest forecast downward.

The purpose of this article will be to provide five additional quarters (15 months) of data to determine whether such a revision is appropriate.

Revised data

Tables 1 and 2 provide updates of the information contained in Tables 1 and 2 of the Autumn 2000 article. Four changes have been made to the latter tables. First, we have added data for the fourth quarter of 2000 and for all four quarters of 2001. Second, in some cases, the relevant statistical authorities have revised their estimates of the figures we reported previously. In those cases, we have provided the revised figures.

Third, we have added information concerning interest rates on five-year Government of Canada bonds. Finally, in the interest of space, we have omitted the estimates of the real rate of interest that relied on information concerning the “standard” inflation rate.

Table 1

Table 1 reports the “raw” data from which some of the real interest rate figures in Table 2 have been calculated. The first column reports the “core rate of inflation” – a measure of the rate of inflation that removes the effects of change in those components of the price index that often move erratically – such as food, energy, and taxes. It is often argued that this measure offers a more reliable predictor of future changes in prices than does the “standard” measure of price inflation.

The second, fourth, and sixth columns report the 5- and 10-year government bond interest rates and 5-year GIC rates net of the core inflation measure.

Finally, columns three, five, and seven report the government bond and GIC rates net of the Bank of Canada’s target rate of inflation of 2 percent. As the Bank has managed to keep the core rate of inflation within a small band around this target for the last six years, it is widely believed that 2 percent is the rate that is expected by most investors. That is, investors are believed to act as if the real rate of interest is the observed, nominal rate less 2 percent.

Table 2

Interpretation of the data

The data in Table 2 indicate that real rates of interest are lowest on the shortest-term investments, GICs and 5-year bonds, and highest on the longest-term investments, 10-year bonds and real rate of interest bonds. This suggests to us that investors believe that the current slowdown in the economy, which has induced central banks to lower interest rates very significantly, may continue for two or three years but will not continue in the long term.

For this reason, we believe that it would be appropriate to adopt a two part forecast of real interest rates. Based primarily on the observed rate on 5-year Government of Canada bonds, we propose to use a rate of 2.50 percent for the first five years of all calculations. Based primarily on the observed rate on 10-year Government of Canada bonds, we propose to use a rate of 3.50 percent for all subsequent years. Note that the latter rate is close to the average real rate of return on GICs over the period 1964 to 1998, (3.58 percent), reported in Bruce, Assessment of Personal Injury Damages, Third Edition, at page 231.

Once again, however, in recognition of the uncertainty facing our economy, we will revisit this question at the end of this year.

Christopher Bruce is the President of Economica and a Professor of Economics at the University of Calgary. He is also the author of Assessment of Personal Injury Damages (Butterworths, 2004).

Derek Aldridge is a consultant with Economica and has a Master of Arts degree (in economics) from the University of Victoria.

Scott Beesley is a consultant with Economica and has a Master of Arts degree (in economics) from the University of British Columbia.

Kelly Rathje is a consultant with Economica and has a Master of Arts degree (in economics) from the University of Calgary.

Selecting the Discount Rate

Posted on September 1, 2000March 24, 2017 By economica

by Christopher Bruce, Derek Aldridge, Scott Beesley, & Kelly Rathje

This article was originally published in the Autumn 2000 issue of the Expert Witness.

One of the most important determinants of the lump sum award for future losses is the discount rate, or real rate of interest. Simply put, this is the rate of interest at which the plaintiff is assumed to invest the award, after the effects of price inflation have been removed.

For example, assume that the court has found that if the plaintiff was to incur a loss today, the value of that loss would be $10,000. But, because the loss will occur one year from now, and the rate of inflation between today and one year from now will be 2 percent, the loss will actually be $10,200.

The court must determine how much the plaintiff will have to invest today in order to ensure that he or she will have $10,200 available one year from now. The discount rate is the interest rate that is used to make this calculation. The purpose of this article is to determine the current value of the discount rate.

We proceed in four steps. First, we distinguish between “nominal” interest rates and “real” interest rates and explain why the latter are generally used in preference to the former. Second, we review a number of alternative methods of measuring the interest rate. Third, we review a number of methods of estimating the expected rate of inflation. Finally, we report the values of these alternative measures for the years 1997-2000 and we conclude with a recommendation concerning the appropriate value to be used today.

Real versus nominal interest rates

There are two methods of calculating the present value of a future loss. The first is to “discount” the loss by the “nominal” rate of interest – that is, by the rate of interest that is observed at financial institutions. The second is to remove the inflationary estimate from the projected loss, to obtain what is called a “real” loss, and then discount that loss by the “real” rate of interest – that is, the nominal rate after the rate of inflation has been removed. The two methods yield identical results.

For example, assume that the nominal rate of interest is 6 percent. The first method of determining the award is to divide $10,200 by 1.06, (that is, by 1 plus the interest rate). That number is found to be $9,623. It can easily be confirmed that if 6 percent of $9,623 is added to $9,623 one obtains $10,200. That is, if the plaintiff was to invest an award of $9,623 at 6 percent, he or she would have $10,200 at the end of one year.

In the second method, one first “removes” inflation, here 2 percent, from both the future loss and the nominal interest rate. In both cases, this is done by dividing by 1.02, (that is, by 1 plus the inflation rate). Thus, as intuition would suggest, the real level of damages is found to be $10,200/1.02 = $10,000. The real interest rate is found to be 1.06/1.02 = 1.0392, or 3.92 percent. (Note that, in the same way that 1.06 is 1 plus the nominal interest rate, 1.0392 is 1 plus the real interest rate.) When $10,000 is divided by 1 plus the real interest rate, 1.0392, one obtains $9,623, exactly the same answer that was obtained using the nominal method.

Economists generally prefer to use the real loss/real interest rate approach when calculating lump sum awards for future losses. The primary reason for this is that real interest rates tend to be much more stable and, therefore, much more easily predicted, than either inflation rates or nominal interest rates.

Alternative measures of the interest rate

Because plaintiffs often have to rely on the investment of their awards to provide a significant portion of their future incomes, it is important that they place their awards in relatively risk-free investments. For this reason, the discount rate is usually based on the rate of return on either long-term government bonds or secure private sector investments. Once a nominal rate has been determined for one of these investments, it is then necessary to determine an expected rate of inflation (over the duration of the investment) in order to calculate the real rate of return.

In this section, we will consider three types of secure investments. In the following section, we will discuss three methods of estimating the expected inflation rate.

Real return bonds The first investment vehicle is Government of Canada real return bonds. These are long-term, secure bonds whose rate of return is denominated in terms of a real interest rate. (That is, the government guarantees that the investor will receive a specified (real) interest rate plus the actual rate of inflation.) There are a number of advantages to using the rate of return on these bonds.

First, when that rate is used, it is not necessary to make a separate projection of the rate of inflation.

Second, these bonds are guaranteed by the government of Canada.

Third, the estimate of the real rate of interest that is obtained by observing the prices at which these bonds are traded in the financial markets provides an objective measure of the real rate of interest that is forecast by sophisticated investors. Note, we are not suggesting that plaintiffs should, or will, invest their awards in real return bonds. Rather, we are arguing that the observed returns on these bonds provides an excellent, objective measure of the expected real rate of return – as these bonds are purchased primarily by individuals who are close observers of money markets and who have a great deal of money at stake when selecting their investments. (Generally, it is pension fund administrators who purchase real return bonds.)

Recently, Ontario revised its Rules of Court concerning the selection of the discount rate. Whereas the previous rule required that the courts use a fixed rate of 2.5 percent, the new rule bases the rate on current observations of the interest rate on real return bonds. For further analysis of Ontario’s new rule, see the accompanying article “Ontario’s Mandated Discount Rate – Rule 53.09(1).”

Guaranteed investment certificates A second approach to the determination of the real discount rate is to identify a measure of the rate of return on a “safe portfolio” of investments (i.e. the kind of portfolio in which a plaintiff could be expected to invest) and to deduct from that rate the expected rate of inflation. We have long recommended that the rate of return on five year guaranteed investment certificates, GICs, be used for this purpose.

Again, as we commented with respect to real return bonds, we are not suggesting that the plaintiff should use his or her award to purchase GICs. Rather, as the types of investments contained in GICs are similar to those that one would expect a prudent investor to purchase, the rate of return on GICs provides an objective measure of the rate of return that plaintiffs can expect to obtain. (Furthermore, as the quoted rate on GICs is net of investment management fees, there is no need to make a separate calculation of the management fee.)

Long-term Government of Canada bonds The rate of return on long-term government bonds can be used as a benchmark against which to measure the returns on other investments. As these bonds are widely held by private citizens (unlike real return bonds) and as they are among the most secure investments available, it would be expected that plaintiffs would never earn a nominal rate of return less than that obtainable from Government of Canada bonds. (If the plaintiff’s investments began to obtain a lower rate of return, the plaintiff could always, easily, transfer his or her investments to government bonds.) Hence, any suggested discount rate must pass the test that it is not lower than the rate obtainable on government bonds. Conversely, we would suggest that the discount rate used should also not significantly exceed the government bond rate, as that would imply that plaintiffs should place their awards in unacceptably risky investments.

Estimating the rate of inflation

The real rate of interest is calculated by removing the effects of price inflation from the nominal rate of interest. As the interest rate is to apply to investments that will continue for many years into the future, the relevant rate of inflation is the average rate that is expected to apply over that future. We will discuss three methods of forecasting this rate.

Current rate of inflation One simple method is to assume that the current rate of inflation will continue into the future. Use of this rate is based on the observation that investors appear to adjust their expectations of the future when current conditions change. Often it is assumed that this shift of expectations occurs with a short “lag,” of six months to two years. But, in periods in which the rate of inflation is not changing quickly, only small errors will be produced if the current rate is used.

Core rate of inflation In Canada, the reported rate of inflation is measured as the change in the price level of a representative “basket” of goods over a 12 month period. For example, the rate of inflation reported for January 2001 will be the percentage change in prices between January 2000 and January 2001.

What this means is that if there is a large, one-time increase in prices in January 2000, measured inflation will be relatively high in each month from January 2000 to December 2000 and then will fall significantly in subsequent months. The reason for this is that the increased price level produced by the January 2000 price increase will continue to be in effect in every future month. Hence, in every month between January 2000 and December 2000, prices will be higher than in the corresponding month a year earlier. Inflation in those months will be correspondingly high.

For example, assume that the CPI had been 100 in every month during 1999, had risen to 110 in January 2000, and stayed at that level for the rest of the year. Then, in every month during 2000 the CPI would be 110, in comparison with 100 in the same month the year before. Hence, in every month in 2000 the rate of inflation would be reported as 10 percent – even though there had not been a price increase since January.

But, when calculating the January 2001 inflation rate, the price level for that month will be compared to a price level (January 2000) that already contains the one-time increase of January 2000. Hence, the measured rate of inflation in January 2001 (i.e. between January 2000 and January 2001) will drop back to the long-run maintainable rate.

In our example, if the CPI remains at 110 in January 2001, inflation between January 2000 and January 2001 will be 0 percent. The one time increase in January 2000 will have had only a temporary impact on the rate of inflation.

What this observation implies is that if we wish to use the current rate of inflation to forecast the long-run rate of inflation, we must first remove the effect of one-time price increases. The Bank of Canada attempts to provide such a measure of long-run price inflation with what it calls its core rate of inflation. In particular, this measure removes movements in the costs of food and energy and movements in prices due to the effects of indirect taxes.

For example, the core rate of inflation would not include the effects of the doubling of oil prices during 2000. Why? Because, although a doubling of prices from $15 a barrel to $30 (and higher) was not completely unexpected, very few observers expect to see prices rise much higher. Hence, even if prices remain at their current level, within 12 months of the initial increases, inflation (the change in the level of prices) will fall. (The increase in oil prices is an example of the one-time increase we discussed above.)

And, of course, if prices should fall back to their pre-2000 levels, short-term inflation will fall even more – perhaps into negative numbers – for the next 12 months. But no one will expect those low levels of inflation to continue any more than they expect the current high levels to continue.

The implication, then, is that the core rate of inflation may be a better indicator of the long-run, expected rate of inflation than is the measure that is usually reported in the press. For this reason, in the tables below, we report both the core rate and the published rate.

The Bank of Canada’s target rate For the last decade, the Bank of Canada’s monetary policy has been directed at producing a rate of inflation of 2 percent (plus or minus 1 percent). As anyone who can remember the 1970s and 1980s can attest, the Bank has been singularly successful in reaching this goal.

Indeed, it has been so successful, that we believe that it can be argued that most investors have come to believe that the long-run rate of inflation will be (approximately) 2 percent. (The Bank itself reports that most financial analysts are predicting inflation rates of approximately 2 percent. See Bank of Canada Monetary Policy Report, November 2000, p. 32.) For this reason, when determining the real interest rate, in the tables below, we report calculations employing an inflation rate of 2 percent.

The data

We present two tables. Table 1 reports quarterly values of the two nominal interest rates – 10-year Government of Canada bonds and GICs – and two of the measures of expected inflation – the standard version and core inflation – for 1997, 1998, 1999, and the first three quarters of 2000. (We do not report the Bank of Canada target rate of inflation, as it did not change over this period.)

Table 1

Table 2 reports the real rates of interest obtained, first, from the real return bonds and, second, from adjusting the two nominal interest rates by each of the three measures of expected inflation. This produces seven measures of the real rate of interest.

Table 2

What these figures suggest is, first, that the interest rate on real return bonds has been remarkably constant over the last three and a half years, rarely deviating very far from the 4.0 to 4.1 percent range until 2000, when it fell to approximately 3.7 percent.

Second, it is seen that the real rate of interest on 10-year government bonds has also fluctuated around 4.0 percent, but with far larger deviations than was seen with respect to the rate on real return bonds. Some of the wider of these deviations can easily be explained, however.

Note, for example, that the low real rates produced in 1998 and 1999 when the 2 percent inflation factor is used may have resulted because a long period of below-2 percent inflation had caused financial markets to believe that the Bank had lowered its target rate. (The conventional measure of inflation exceeded 2.0 percent only once between the first quarter of 1996 and the third quarter of 1999, when it was reported to be 2.1 percent in the first quarter of 1997.) If the markets had come to expect inflation rates of 1.5 percent in 1998 and 1999, for example, most of the real rates in those years would have been close to 4.0 percent.

The relatively high rates found in 2000 when long-run bond rates are discounted by core inflation, and the relatively low rates found in that year when they are discounted by the standard measure of inflation, could both be “explained” if it was found that financial markets had begun to accept the Bank of Canada’s statement that it was targeting a long-run inflation rate of 2 percent.

The consistently low rates found on GICs, however, are disconcerting. Over the entire period reported in Table 2, and for a number of years prior to that, the rates of return on GICs were significantly lower than those on government bonds. This suggests that plaintiffs would be extremely unwise to invest in GICs for the foreseeable future.

We conclude, therefore, that current estimates of the discount rate should be based on the rates observed on real return bonds and on long-term Government of Canada bonds. Arguably, these rates fluctuated around 4.0 percent for most of the last four years. They have, however, fallen slightly during 2000.

This raises the question of whether 2000 is an aberration, or whether the recent decline in real rates is the beginning of a long-term trend. Some evidence that the decline is expected to be short-lived comes from the Alberta government’s Budget 2000 documents. There, it is reported that nine respected forecasting agencies predicted an average interest rate on Government of Canada 10-year bonds of approximately 6.21 percent (over the years 2000-2003). As it is unlikely that those agencies would have forecast an inflation rate in excess of 2 percent, implicitly they have forecast a real rate of interest of approximately 4.1 percent.

In this light, we believe that a rate of 4.0 percent is the best, current estimate of long-run real interest rates. However, Economica will be monitoring movements in the interest rates on real return and 10-year Government bonds closely. If bond rates do not rise relative to the rate of inflation in the near future, we will be revising our real rate of interest forecast downward.

Christopher Bruce is the President of Economica and a Professor of Economics at the University of Calgary. He is also the author of Assessment of Personal Injury Damages (Butterworths, 2004).

Derek Aldridge is a consultant with Economica and has a Master of Arts degree (in economics) from the University of Victoria.

Scott Beesley is a consultant with Economica and has a Master of Arts degree (in economics) from the University of British Columbia.

Kelly Rathje is a consultant with Economica and has a Master of Arts degree (in economics) from the University of Calgary.

Ontario’s Mandated Discount Rate – Rule 53.09(1)

Posted on September 1, 2000March 24, 2017 By economica

by Christopher Bruce

This article was originally published in the Autumn 2000 issue of the Expert Witness.

Recently, Ontario changed its Rules of Court concerning selection of the discount rate. Previously, Rule 53.09(1) required that the courts use a real interest rate of 2.5 percent when discounting future earnings.

The new rule divides the future into two periods – the next 15 years, and beyond 15 years. In the first period, Rule 53.09(1) requires that the courts use the rate observed on real return bonds for the 12 months ending August of the year preceding the date of calculation, less one percent, rounded to the nearest one quarter percent.

For example, as the average rate for the 12 months ending August 2000 was 3.87 percent, all calculations performed in 2001 must use a discount rate of 2.75 percent – that is, 3.87 minus 1.00 rounded to the nearest 0.25.

In the second period, for losses beyond 15 years into the future, 2.5 percent is still to be used.

The wording of Rule 53.09(1) clearly states that the figure obtained by deducting 1 percent from the rate on real return bonds is to represent the discount rate. The committee that recommended the changes to Rule 53.09(1), (the Subcommittee of the Civil Rules Committee on the Discount Rate and Other Matters), deliberately selected this wording.

It was their view that because real return bonds are not traded very frequently and because they receive “unfavourable tax treatment,” “economic and risk factors” biased the reported rate upwards. That is, it was felt that a risk free investment would have a lower rate of return – by 1 percent – than that reported for real return bonds.

I do not agree with the committee’s conclusions on this matter. The committee seems to have been confused about the rationale for using the rate on real return bonds. As was indicated in the article “Selecting the Discount Rate” in this issue, the proposal is not that plaintiffs purchase real return bonds. Rather, the rate of return on those bonds is to be used as an objective indicator of the forecast that sophisticated investors are making of the real rate of interest.

This is not to say that some discount should not be made for the fact that so few of these bonds are bought and sold. But a discount of 1 percent seems well out of line. This was seen clearly in the last section of “Selecting the Discount Rate,” in which recent statistics concerning real interest rates in Canada were summarised.

There it was reported that real rates of interest on risk-free Government of Canada bonds have been very similar to the rates reported on real return bonds in the last three years. It appears that the committee was reluctant to choose an interest rate that would differ significantly from the previous mandated rate of 2.5 percent.

Interestingly, the Ontario Court of Appeal, in Martin v. Listowel Memorial Hospital (Docket C31222, November 1, 2000), concluded that the current real rate of interest is approximately 4 percent, not the 2.75 percent implied by its own Rules of Court. Indeed, in the Martin decision, the Court seemed to signal that it was willing to accept evidence concerning the discount rate on a case-by-case basis – hardly a ringing endorsement of the newly-established Rule 53.09.

Christopher Bruce is the President of Economica and a Professor of Economics at the University of Calgary. He is also the author of Assessment of Personal Injury Damages (Butterworths, 2004).

Selecting the Discount Rate

Posted on September 1, 1996March 24, 2017 By economica

by Christopher Bruce

This article first appeared in the autumn 1996 issue of the Expert Witness.

The discount rate is the interest rate at which it is assumed plaintiffs will invest their awards in order to replace their future streams of losses. As was explained in the first issue of this newsletter, it is the “real” rate of interest – or observed rate of interest net of the expected rate of inflation – which most financial experts prefer to use for this purpose.

In six provinces, the discount rate has been set by regulation. In the remaining four, including Alberta, however, the expert must provide evidence concerning the forecasted value of the real interest/discount rate. The purpose of this article will be to review a number of techniques for obtaining such a forecast and to provide an estimate of the real rate of interest based on the most reliable of these techniques.

The article will be divided into three sections. In the first, I list the rates in the six provinces which mandate a discount rate. In the second section, I summarise three methods which have been used to forecast real interest (discount) rates and identify the strengths and weaknesses of each of those methods. Finally, I select one method and use it to select a discount rate for use in Alberta.

Mandated Discount Rates

Mandated discounted rates in Canada
Province	Discount Rate
British Columbia	3.5% (cost of care)
British Columbia	2.5% (loss of income)
Saskatchewan	3.0%
Manitoba	3.0%
Ontario	2.5%
New Brunswick	2.5%
Nova Scotia	2.5%
Prince Edward Island	2.5%

The discount rates shown in the previous table have been mandated in Canada.

Three Methods for Determining Discount Rates

1. The historical approach: The approach which, implicitly, has been favoured by those provinces which have mandated their discount rates is to assume that the average rate which has been observed in the past will continue into the future. Typically, those who use this approach rely on the real interest rates which have been reported over the entire post-World War II period. What analysis of these rates indicates is that real rates were fairly stable over the period 1950-1970, at approximately 3 percent. During the oil crisis, of the early 1970s, real interest rates fell, sometimes becoming negative. Towards the end of that decade, however, they began to rise again and it appeared that they would return to their historical level. But the rise continued beyond 3 percent and since 1983 real interest rates have consistently remained above that level. Indeed, real interest rates have remained above 4 percent for so long that it is now difficult to justify the use of a rate lower than that. At the very least, any expert who attempted to rely on the historical 3 percent average to forecast future rates of interest would have to explain why the 1980s and 1990s were such an anomaly.

2. Forecasting agencies: There is a small number of consulting firms in Canada which provide forecasts of such economic variables as GNP, the unemployment rate, and inflation. They will also forecast other variables, including the real rate of interest. Extreme caution must be used when employing these firms’ long-term forecasts, however. First, the mathematical models which they employ were built specifically to make short- term forecasts. Second, long-term forecasts cannot be made without imposing assumptions about many factors which are outside the mathematical models developed by these agencies, such as foreign interest rates, exchange rates, and government monetary and fiscal policy. Finally, private forecasters have little incentive to produce accurate long-term forecasts. A consulting firm’s reputation will not hinge in any way on the accuracy of its current forecasts concerning, say, the level of unemployment in 2020. The forecasts which customers use to evaluate the agencies’ accuracy are those which have been made into the near future, not the distant future. Hence, it is forecasts of one or two years on which consulting firms concentrate their resources. The real rate of interest, on the other hand, must commonly be forecast twenty or thirty years into the future.

3. Market rates: The third source of information concerning future real rates of interest is the money market. When an investment firm which believes that inflation will average 2 percent per year purchases 20 year bonds paying 6 percent, it is revealing that it expects the real rate of interest will average 4 percent over those 20 years. (The real rate of interest is the 6 percent observed, or “nominal,” rate of interest net of the 2 percent inflation.) Thus, if we knew the rate of inflation which investors were forecasting, that forecast could be used to deflate the nominal rates of interest observed in the market in order to obtain the implicit, underlying real rates. At the moment, such forecasts can be obtained with some accuracy. Not only do surveys of investors conclude that there is considerable agreement among them with respect to their forecasts of inflation – generally between 2 and 3 percent – but we know that the government is strongly committed to maintaining a long-run inflation rate below 3 percent. Thus, we can be confident that investors predict real rates of interest which are no less than the observed, nominal rates less 3 percent. (For information concerning the long-run expected rate of inflation, see Bank of Canada, Monetary Policy Report, May 1996.)

Alternatively, the Canadian government has for some time issued bonds which are denominated in terms of real interest rates, (real rate of interest bonds, or RRBs). By observing the rates of return at which these bonds sell, the real rate of interest which investors believe will prevail over the future can easily be determined. There are two drawbacks to the use of market interest rates to forecast future real rates of interest. First, the rate which is obtained from this method has not been stable, but has generally fluctuated between 4 and 6 percent since 1983. Hence, no definitive conclusion can be drawn. Second, as very few RRBs have been issued, the rates of return which they have obtained may not accurately reflect the rates in the market as a whole.

Forecasting the Discount Rate

Of the three techniques for forecasting real interest rates discussed in the previous section, the least satisfactory is the first one, based on historical rates. As those rates have varied so widely since the early 1970s, they convey little reliable information concerning the future. Of the remaining two, most economists prefer the market-based technique. A simple analogy will explain why.

Imagine that you wished to determine the average price which potential purchasers were willing to pay for twenty-year old, three bedroom bungalows in Edmonton. One approach would be to conduct a telephone survey of Edmontonians, asking them what they would be willing to pay for such homes. A second approach would be to observe the actual prices at which such homes sold in Edmonton. Clearly, the second approach is preferable. Why? Because rather than asking individuals how they think they will behave in some hypothetical situation, it observes how individuals actually behave when they have to commit large sums of money to their decisions.

Similarly, economists who are asked to forecast long-term interest rates recognise that little is at stake should those forecasts be in error. Whereas those who are involved in purchasing long-term bonds recognise that the smallest error can result in losses of tens of thousands, even millions of dollars. For this reason, Economica prefers to rely on the interest rates observed in the money market, rather than on surveys of economic consultants, to determine the long-run discount rate.

The following table summarises money market estimates of the long-run real rate of interest for three series: the rate of return on trust company five year guaranteed investment certificates, the interest rate on Government of Canada 10-year bonds, and the rate of return on RRBs. In each case, the figure represents the average of the rates reported in the second quarter (April-June) of 1996, net of the forecast rate of inflation. Two alternative real rates have been calculated for the GICs and the 10-year bonds: the first uses a forecasted rate of inflation of 2 percent and the second a rate of 3 percent. (The figure for RRBs is the same in both scenarios as the observed, market rate is already net of the rate of inflation.)

Real Rates of Return on Selected Long-term Investments: Canada 1996
Investment	2% Rate of Inflation	3% Rate of Inflation
Trust Company 5-year GICs	4.5%	3.5%
Government of Canada 10-year bonds	5.6	4.6
Real rate of return bonds	4.7	4.7

The figures in this table suggest that investors currently anticipate that the real rate of interest will fall somewhere between 3.5 and 5.0 percent. At Economica, we employ the mid-point of this range: 4.25 percent.

Christopher Bruce is the President of Economica and a Professor of Economics at the University of Calgary. He is also the author of Assessment of Personal Injury Damages (Butterworths, 2004).

What is a “Discount Rate”?

Posted on March 1, 1996March 23, 2017 By economica

by Christopher Bruce

This article first appeared in the spring 1996 issue of the Expert Witness.

Alberta is one of only four provinces in which the discount rate is not mandated. As I argued in Ontario’s 2 1/2% Solution (Canadian Bar Review, December 1982) this means that we are able to react much more flexibly to changes in the economic situation than are the six provinces whose rates are set by a central authority. Indeed, the superiority of Alberta’s approach is seen in the fact that whereas interest rates have varied significantly over the last 15 years, not one of the provinces with mandated rates has adjusted that rate.

Nevertheless, the lack of a mandated rate does carry the drawback that an onus is placed both on financial expert witnesses and on counsel to understand how the discount rate is determined and to identify whether economic forces have changed in such a way as to make previous assumptions about that rate obsolete. The purpose of this article will be to provide a basic explanation of what the discount rate is and of how it works. In a second article, I identify a number of alternative methods of forecasting the discount rate and use what is generally considered to be the preferred method to identify such a rate for Alberta.

Assume that a plaintiff will require dental work one year from now. If that work was carried out today, it would cost $1,040. The question which faces the legal system is: “How much does the plaintiff have to be compensated today, in order to ensure that he/she will have enough money to pay for this procedure one year from now?” The answer to this question depends, first, upon the effect of the rate of inflation on the cost of the procedure; and, second, upon the rate of interest at which the plaintiff can invest his/her award.

The effect of the rate of inflation is relatively straight forward. If, for example, the cost of dental procedures is expected to increase by 2.5 percent in the next year, this plaintiff will need $1,040 increased by 2.5 percent one year from now. That is, the amount required will be:

$1,040 + (2.5% x $1,040)
= (1.00 x $1,040) + (0.025 x $1,040)
= (1.00 + 0.025) x $1,040
= 1.025 x $1,040
= $1,066

In short, to find the inflated value one year from now, the current value (here, $1,040) is multiplied by 1 plus the rate of inflation (here, 1.025).

The second step is to determine how much has to be paid to the plaintiff today in order to ensure that he /she will have $1,066 one year from now. Assume for this purpose that the rate of interest which plaintiffs can expect to receive on secure investments is 6.6 percent per annum. It is intuitively clear that $1,000 invested at this rate will yield $1,066 (the desired amount) one year from now. Formally, this $1,000 figure, which is called the present discounted value or commuted value of $1,066, can be derived in the following way: Call the present discounted value $P. When $P is invested at 6.6 percent interest, we want it to yield $1,066. Hence,

$P + (6.6% x $P) = (1.00 x $P) + (0.066 x $P)
= (1.00 + 0.066) x $P
= 1.066 x $P
= $1,066

That is, we know that

1.066 x $P = $1,066

Therefore, to find $P, we need only divide both sides of this equation by 1.066, to obtain

$P = ($1,066 / 1.066)
= $1,000

Remembering that the $1,066 figure in this equation was found by increasing the current cost of the dental procedure, $1,040, by the rate of inflation, 2.5 percent, it is now seen that amount which must be paid to the plaintiff today, $P, may be obtained from the formula:

$P = $1040 x (1.025 / 1.066)
= $1,040 x (1.00 / 1.04)
= $1,000

What this set of calculations is intended to show is, first, that $P can be found by multiplying the current cost of the expense to be compensated, here $1,040, by (1 + inflation), here 1.025, divided by (1 + interest), here 1.066. Second, (1.025 divided by 1.066) can be replaced by (1.00 divided by 1.04). This 1.04 figure is known by economists as the real rate of interest or the discount rate. This is the figure which expert witnesses use to determine the present, or lump sum value of a future cost. It is called the real rate of interest because it was calculated by dividing 1.066 by 1.025; that is, (1.025/1.066) = 1.00/(1.066/1.025) = (1.00/1.04). Dividing (1 + interest) by (1 + inflation) in this way has the effect of “netting out” the impact of inflation from the observed, or nominal, interest rate, leaving only that element of interest payments which is independent of inflation – the “real” rate of interest.

Economists and other financial experts have used the real rate of interest to discount future losses because it has been less volatile than the nominal rate of interest. (The nominal rate increases and decreases with the rate of inflation while the underlying real rate remains stable.) Recently, however, the real rate has been almost as variable as the nominal rate. Nevertheless, because the courts have become accustomed to the use of the real rate, the Expert Witness will follow that convention.

Christopher Bruce is the President of Economica and a Professor of Economics at the University of Calgary. He is also the author of Assessment of Personal Injury Damages (Butterworths, 2004).

Economica

Assessment of damages in personal injury and fatal accident litigation

Tag: Discount Rates