Month: December 2012

Winter 2012 issue of the Expert Witness newsletter (volume 16, issue 1)

Posted on By economica

Contents:
In every personal injury or fatal accident case in which the plaintiff’s loss continues into the future, it is necessary to calculate the rate of interest at which the damages will be invested. This interest rate is commonly called the discount rate. In this issue of the Expert Witness, we provide two articles concerning the determination of this rate.

The Discount Rate Simplified

  • In the first, which was written collaboratively by Christopher Bruce, Laura Weir, Kelly Rathje, and Derek Aldridge, we begin by setting out a number of criteria that we believe should be met when selecting the discount rate. We ultimately conclude that a portfolio of Government of Canada bonds of varying maturity dates meets our criteria. We then argue that forecasts of Government of Canada bond rates that are based on historical statistics are unreliable for many reasons. Finally, we argue that the rates of return that are currently available on government bonds represent reliable predictions of future rates. Short-term interest rates can perform this role because they represent rates that are actually available currently; and long-term rates reflect the forecasts that have been made by sophisticated financial institutions that have substantial investments in the market.

Implied Rates of Return on Structured Settlements

  • In the second article, Derek Aldridge and Christopher Bruce contrast our recommended discount rates with those used by one important set of sophisticated investors, the insurance companies who write structured settlements. They find that our recommended rates are greater than those being offered by these companies, suggesting that our rates may be too high.

Implied Rates of Return on Structured Settlements

Posted on By economica

by Derek Aldridge & Christopher Bruce

The purpose of a lump sum award in a personal injury or fatal accident case is to provide a fund that, when invested, will generate a stream of benefits equal to the plaintiff’s future stream of losses. One method of generating such a stream would be to purchase a life annuity. This, for example, is what is anticipated by Section 19.1 of the Judicature Act (RSA 2000) when it provides that:

(2)  On application by any party to a proceeding, the Court may order that damages awarded be paid in whole or in part by periodic payments…

This type of periodic payment has come to be known as a structured settlement annuity. Such annuities are sold by insurance companies. When calculating the price it is going to charge for an annuity, the insurer determines how much it would have to invest, at current interest rates, in order to generate a stream of income at least equal to the required periodic payments. For example, if it had promised to pay $10,000 per year indefinitely , and the rate of interest that it thought it could earn was 10 percent, it would charge at least $100,000 – as $100,000, invested at 10 percent per year, would generate a stream of income of $10,000 per year.

Conversely, therefore, if we observe the lump sum that an insurance company charges for an annuity that promises a specified stream of payments, we can calculate the rate of interest that the insurance company expects to obtain on the investment of that sum. For example, if it was observed that the company had charged $100,000 for a periodic payment of $10,000 per year (indefinitely)¹, we would be able to calculate that the rate of return it expected to obtain on investment of that $100,000 was at least 10 percent.

We have used this principle to calculate the rate of return that insurers expect to obtain on a series of standard structured settlements. By contrasting these rates of return with the rates that Economica has been using, we can check whether Economica’s rates are consistent with those that sophisticated investors – insurance companies – expect to earn on low-risk investments.

With the assistance of Heber Smith, of Smith Structured Settlements (www.structuredsettlements.ca), in August 2011 we obtained quotes on an annuity that provided payments of $1,000 per month to a male plaintiff. These quotes were for

  • three different ages of plaintiffs: 20, 35, and 50;
  • two different termination dates: the plaintiff’s age 60 and his age of death; and
  • two different assumptions concerning inflation indexation: one in which the insurer increased the annual payment each year by the rate of consumer price inflation and one in which the payment was increased each year by a fixed 2 percent.

We report the quotes that we obtained for twelve different scenarios in columns 6 and 8 of the table below. As an example of how to read this table, the $127,064 figure in column 6 of the first row in the table, indicates that we were quoted a price of $127,064 to purchase an annuity that paid $1,000 per month, increasing at the rate of consumer price inflation, from the plaintiff’s age 50 to his age 60. Similarly, it is seen from column 8 of the first row that that annuity would have cost $121,255 if the payments had been adjusted by 2 percent per year instead of by the prevailing rate of inflation. (If we assume that insurers believe that inflation will be 2 percent on average, the difference be $5,809 difference between columns 6 and 8 in the first row is a “premium” the insurer charges to compensate it for taking the risk that inflation might prove to be higher than 2 percent.)

The comparable figures in columns 6 and 8 of the third row of the table report the cost of an annuity that extends to the end of the plaintiff’s life, instead of to age 60 (as in the first row). The figures in the third row would be relevant if an annuity was being purchased to pay for costs of care, instead of for loss of earnings (first row). The remaining rows in the table report the costs of annuities paying $12,000 per year to a 20-year old and a 35-year old.

Given the quotes reported in columns 6 and 8, we were able to calculate the real rate of interest (interest rate net of a two percent expected rate of inflation) the insurance company was expecting to receive from investment of each annuity. These rates are reported in columns 7 and 9, with the figures in column 7 referring to the quotes in column 6 and the figures in column 9 referring to the quotes in column 8. As an example, the figure of -0.95% in column 9 of the first row indicates that the insurance company anticipated that it would receive a nominal interest rate of approximately 1.05% (i.e. 1.05% nominal interest – 2.00% inflation = -0.95% real rate of interest, or discount rate).

Of the twelve discount rates reported in the table, only one – the 2.10 percent rate of return in column 9 of the second row – exceeds the lowest rate used by Economica, as reported in Table 2 of the first article in this newsletter – 1.80 percent on investments of less than four years; and most of the remaining discount rates are significantly lower than the rates that we recommend.

The result is that the present discounted values quoted by insurance companies for the purchase of structured settlements are considerably higher than the comparable values that would have been calculated by Economica. The latter values are reported in column 4 of the table. It is seen in column 4 of row four, for example, that whereas Economica would have calculated that a plaintiff would need $277,538 to replace $12,000 per year from age 20 to age 60; the quote we received for a structured settlement was $506,890 – 82.6 percent more.

The differentials are even greater if we use the discount rate that some other expert economists have recommended – 3.50 percent. In the fourth row of column 5, for example, we report that the present value of $12,000 from age 20 to age 60 would be $252,895 if 3.50 percent is used – less than half of the $506,890 that we were quoted for a structured settlement.

To conclude: in every case, the present values that we would estimate using our discount rate assumptions are considerably lower than the actual cost that a plaintiff would incur if he were to buy an annuity to fund his future losses. This is very strong evidence in support of the claims that we have made over the last several years that our discount rate approach is a conservative one. Based on the costs to purchase structured settlement annuities, and the plaintiff’s ability to demand that his/her loss be funded using this “periodic payment” approach (given Section 19.1 of the Judicature Act), it follows that any reasonable change to our discount rate approach would be to use lower rates, not higher (as some other experts have argued).

Acknowledgment

As noted above, Heber Smith, of Smith Structured Settlements generously provided us with quotes on various annuities which we used in the creation of this article. On previous cases, we have worked together with Mr. Smith when the plaintiff’s lawyer chose to argue that damages should be satisfied by periodic payments (in accordance with Section 19.1 of the Judicature Amendments Act), rather than a conventional present value. An advantage of having future losses assessed in this manner is that it removes the subjective nature of opinions concerning the discount rate. Instead of relying on opinion concerning the rate of return that a plaintiff will earn on his or her investments, we can determine precisely how much it will cost the plaintiff to purchase annuities to fund the future losses.

Smith Structured Settlements serves the personal injury community as an annuity brokerage specializing in the preparation of fee-based Section 19.1 damages reports. Should you wish to investigate such an option they may be reached at www.structuredsettlements.ca.

 

 

Footnote:

  1. Of course, structured settlements never continue indefinitely. We use this example because of its mathematical simplicity. [back to text of article]

The Discount Rate Simplified

Posted on By economica

by Christopher Bruce, Laura Weir, Derek Aldridge, and Kelly Rathje

In every personal injury or fatal accident case in which the plaintiff’s loss continues into the future, it is necessary to calculate the rate of interest at which the damages will be invested. This interest rate is commonly called the discount rate, and it is calculated as the nominal (or observed) rate of interest net of the expected rate of price inflation.

As Alberta has no mandated discount rate, the determination of that rate is left to the courts. In this article, we propose to offer a simple technique for identifying this rate.

We proceed in two steps. First, we discuss the criteria that we believe must be met when selecting the discount rate. Second, we apply these criteria to the relevant data, to make that selection. In a separate article following this one, Derek Aldridge and Christopher Bruce contrast the rates that we propose with those that are available on structured settlements.

1. Criteria

The first step in selecting a discount rate is to recognise that the plaintiff is expected to invest his or her award in such a way that the stream of income generated from that award will exactly reflect the stream of losses that the plaintiff has suffered. If the plaintiff has lost $50,000 per year for twenty years, investment of the lump-sum award should produce $50,000 per year, with the principal being exhausted by the end of the twentieth year.

As this stream of investment income is intended to replace a significant portion of the plaintiff’s lifetime earnings, the courts have ruled that the lump-sum should be invested in low-risk financial instruments. Hence:

The discount rate must be based on an investment portfolio that is of low risk.

Although this requirement does not mean that the plaintiff must put all of his or her award into government bonds or guaranteed investment certificates (the lowest-risk investments available), we argue that the interest rate available on those investments provides the most reliable indicator of the rate of return required by the courts.

The plaintiff may well include in his/her portfolio non-government or non-guaranteed investments, such as corporate bonds, mutual funds, and blue chip stocks; but, that the returns on such investments are higher than those obtained from government bonds results primarily from the higher level of risk associated with them – as was seen with devastating results in the post-2008 stock market crash.

The difference between the rate of interest on a government bond or a GIC and, say, a corporate bond is a measure of the compensation that investors demand for accepting a higher degree of risk on the latter investment than on the former. Once that level of “compensation” is deducted, the net, risk-free, interest rate is approximately the same on both. Hence:

The rates of return on Government of Canada bonds and GICs represent reliable indicators of the rate of interest sought by the courts.

Once it has been decided that it is government bond and GIC rates that are to be used, it is necessary to select from among the various options that are available to the plaintiff. Financial advisors recommend that, in order to reduce risk, investors should purchase a mix of bond durations. In that way, if interest rates should rise, investors can sell their short-term bonds and purchase newly-issued bonds at the higher rates; and if interest rates should fall, although investors will have to accept reduced interest rates on any new investments, they will still experience relatively high rates on their long-term (locked-in) investments. Hence:

Plaintiffs should purchase a mix of short-, medium-, and long-term investments.

If the duration of the plaintiff’s loss is less than ten years, the plaintiff will minimize risk by purchasing investments that have durations that mature on the dates on which the losses are incurred. For example, a one-year bond might be purchased to replace the loss one year in the future, a two-year bond to replace the loss two years from now, etc. Hence:

For losses that will occur in the next ten years, the relevant interest rate for any year is the rate of interest on a Government of Canada bond (or GIC) that has a term equal to that number of years.

But if the plaintiff’s loss extends for more than ten years, it will be wise to adopt an investment strategy in which bonds are purchased for shorter terms than the duration of the loss, and then re-invested periodically. To replace a loss twenty years from now, for example, the plaintiff might purchase five-year bonds today and re-invest the returns every five years until the funds were needed. If a similar practice is followed for every duration of loss, the risk that interest rates will rise or fall, relative to what is expected at the time of the initial investment, will be minimised.

Such a strategy, of rolling over short-term investments in order to generate a long-term return, means that the effective discount rate over the term of the investment will be determined not only by the rates that are available today but also by rates that will become available in the future. Thus, the court must predict what those future rates will be.

Contrary to what many experts argue, this prediction can be made simply and with confidence: the most reliable prediction of the rate of interest that will prevail in the long-run is that it will equal the rate of return currently available on long-run bonds. For example, if the current rate on 15-year government bonds is 3.0 percent, the best prediction of the rate of return that will prevail over the next fifteen years is 3.0 percent.

The argument for basing the prediction on this rate can most easily be understood by showing that the contrary cannot be true. For example, it might be argued that “as interest rates are unusually low today, it can be expected that they will eventually rise above current rates.” If this argument is correct, then individuals who wished to invest their funds for long periods of time (for example, individuals who are saving for their retirement) would not purchase long-term bonds today – they would purchase short-term bonds while waiting for interest rates to rise, and then purchase bonds at the new, higher rates once the interest rate had risen.

But if investors behaved this way, the demand for long-term bonds would decrease; and when demand for a bond decreases, its interest rate rises. (Issuers have to raise the rate of return in order to attract investors.) That is, if investors predict that the long-term interest rate will exceed the rate currently available on long-term bonds, they will act in such a way as to drive up the interest rate on long-term bonds. A bond rate that is less than the expected rate cannot be maintained.

Similarly, if investors believed that interest rates were about to fall, they would sell their short-term bonds and purchase long-term. But this would decrease the demand for short-term funds, driving up short-term interest rates, and increase the demand for long-term funds, driving down long-term interest rates.

In short, if the rate of interest that is currently available on long-term bonds is different from the rate that investors expect will prevail in the future, the long-term bond rate will change “towards” the rate that investors predict. As a result, the interest rate available on long-term bonds will always adjust until it equals the rate that investors predict will prevail in the long run. And, as investors have a strong incentive to make correct predictions about the bond market, it is likely that their predictions are the best that are available. Hence, we conclude that:

The best predictor of the rate of interest that will prevail in the long-run is the rate of interest that is currently offered on long-term bonds.

Finally, as we noted in the introduction to this article, the discount rate is found by netting out the forecasted rate of price inflation from the observed nominal rate of interest. Hence, before the discount rate can be determined:

The long-run rate of price inflation must be forecast.

Fortunately, there is a clear consensus that the long-run rate of inflation in Canada will be two percent. This consensus has developed because, since the early 1990s, the Bank of Canada has not only set two percent as its long-run target, it has both met that target and expressed satisfaction with the results of its policy.

That participants in the “money markets” have come to accept that the Bank will achieve this goal over the long-run is seen in two surveys of business leaders that have been conducted annually since 1994. Consistently, respondents have reported that they expect the long-run rate to be 2.0 percent. Indeed, not only has the average, expected rate been 2.0 percent in most years that the surveys were conducted, the variation of responses “around” 2.0 percent has decreased continuously. Hence:

There is a strong consensus that, in the long run, the rate of inflation will average 2.0 percent in Canada. Hence, the discount rate can be found by reducing the forecasted nominal rate by 2.0 percent.

2. Data

In Figure 1 and Table 1 we report the annual rates of return that have been available since 1995 on five Government of Canada bonds: 2-, 5-, and 10-year bonds, long-term bonds (an average of bonds with a maturity date longer than 10 years), and “real rate of return” bonds (bonds whose rates of return are stated net of inflation). It is seen there that both nominal and real interest rates on Government of Canada bonds have decreased almost continuously since the Bank of Canada introduced its policy of targeting a two percent rate of inflation. Whereas real interest rates were between 4.5 and 7.5 percent in 1995, they have fallen below one percent on most bonds, and even below zero percent on some, in recent years.

 

 

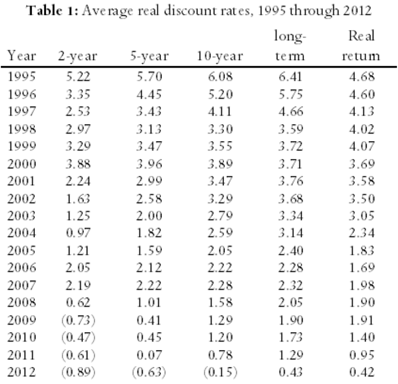
What these figures indicate is that investments in government bonds are unlikely to provide real rates of return above zero percent over the next five years; that bonds of five to ten year durations are unlikely to produce rates in excess of 1.0 percent; and that the market expects long-term real interest rates on government bonds to be less than two percent.

Nevertheless, in recognition of the fact that current rates are at a historical low, we have left our assumed rates at the same values we have employed for the past five years. Those rates, which we report in Table 2, are: 1.8 percent per year on funds invested for three years or less; rising in equal increments to 3.0 percent per year on funds invested for more than fifteen years.

 

leaf

Christopher Bruce is the President of Economica and a Professor of Economics at the University of Calgary. He is also the author of Assessment of Personal Injury Damages (Butterworths, 2004).

Derek Aldridge is a consultant with Economica and has a Master of Arts degree (in economics) from the University of Victoria.

Kelly Rathje is a consultant with Economica and has a Master of Arts degree (in economics) from the University of Calgary.

Laura Weir is a consultant with Economica and has a Bachelor of Arts in economics (with a minor in actuarial science) and a Master of Arts degree from the University of Calgary.