This article first appeared in the spring 2008 issue of the Expert Witness.
Our readers will recall that every year or two we review our standard discount rate assumptions and publish our findings. It is time to repeat this exercise.
In the Summer 2006 issue of the Expert Witness, we reported that real rates of interest (that is, the rates of return net of inflation) had increased slightly from those outlined in our Summer 2005 article. We responded by increasing our forecast of the short-term (one to six years) real rates of interest. Our forecasted interest rates for the medium to long-term (seven to 15 years or more) remained unchanged – although these rates were slightly higher than the observed real rates of return on Government of Canada bonds, long-term real rate of return bonds, and the long-term rate mandated in Ontario. (Higher rates lead to lower present values, so our estimates can be considered conservative.)
In our 2006 article we specified our assumptions for real interest rates for periods ranging from one-year to 15 years or more. Our assumptions were based on the observed rates of interest on Government of Canada bonds of various terms. We now have more rates to observe and we see that these rates have continued their long-term downward trend. Real rates of interest for five bond series over the last 14 years are depicted in the figure below (with the rates for 2008 estimated using an average of the January through June interest rates).
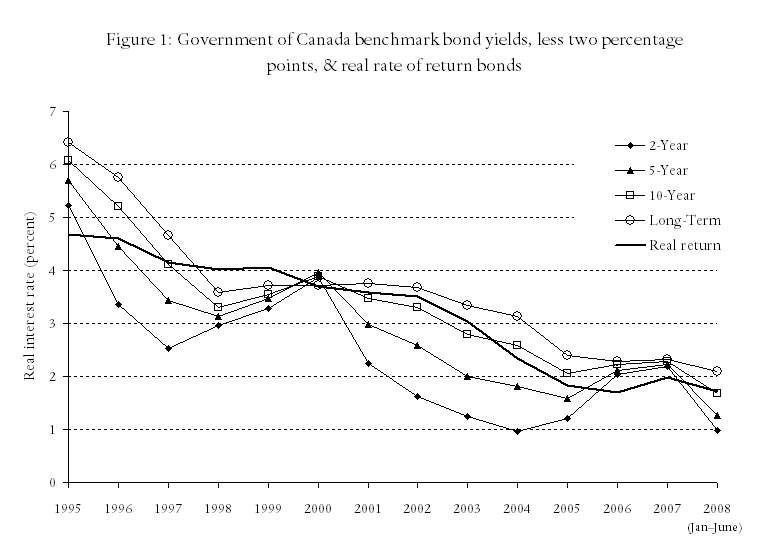
From the figure we see that real rates have decreased slightly from their 2006 and 2007 levels. However, the decrease in real interest rates is not sufficient to warrant a change in our discount rate assumptions. In particular, we note that the average real rates for the past 12 and 24 months are very similar to the corresponding averages at the time we wrote the previous article. One exception is the long-term rate, whose 24-month average (2.23 percent) is a third of a percent less than the corresponding 24-month average at the time of our previous article.
Although we do not show the comparable interest rates on guaranteed investment certificates (GICs), we have examined them and they are consistently lower than the rates of return on bonds. For example, the rate currently offered for 5-year GICs is approximately three percent, corresponding to a real rate of only one percent.
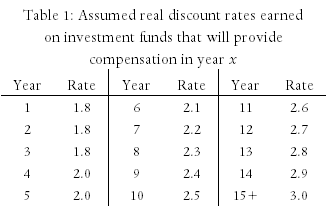
Our discount rate assumptions, unchanged from our 2006 article, are shown in the table below.
Over the years, our approach to forecasting an appropriate discount rate has been criticized by other economists who prefer to rely on historical interest rates in making their forecasts. Below, we address some of these critiques and provide support for our approach.
Our approach, often called the “conservative investment” approach (which assumes a plaintiff will use his damage award to purchase a financial instrument with an appropriate term to maturity and hold that instrument to maturity), has been criticized by other economists who argue for a “market-based” approach (that assumes a plaintiff will buy and sell bonds as interest rates vary instead of holding the bond to maturity). One of us (Bruce) addressed this issue in an article written for the Spring 2007 issue of the Expert Witness entitled “Forecasting the long-term interest rate on Government of Canada bonds: “market-based” versus “conservative” investment“. We summarize his conclusions here as this issue continues to arise.
Some economists suggest that our approach ignores the price changes resulting from changes in the interest rate within the bond market, arguing for the market-based approach that assumes the plaintiff can earn a higher rate of return by actively buying and selling bonds as interest rates change. As a simple example, suppose a plaintiff will incur a loss of income of $100,000, 20 years from now. The conservative approach assumes that he will purchase a 20-year bond, paying five percent in interest per year, for $37,689 and redeem it at maturity for $100,000 to fund his loss in that year.
Assume, however, that the interest rate decreases to four percent one year after purchase. The market-based approach suggests that at four percent, the plaintiff could sell his bond (that has 19 years left to maturity) for $47,464 (= $100,000/1.0419) and earn $9,775 (= $47,464 – $37,689) in profit, for an effective rate of return of 25.94 percent in one year. However, this is actually not a profit because the plaintiff still has to purchase a 19-year bond (at a cost of $47,464) to fund his $100,000 loss of income 19 years from now. Thus, there is no real benefit to actively trading bonds as the interest rate changes.
In addition to the fact that the effective rates of return under the market-based approach are illusory, effective rates of interest are extremely variable. For example, a publication by the Canadian Institute of Actuaries entitled Report on Canadian Economic Statistics 1924-2005 indicates that the 10-year average (1996-2005) effective real rate of return on long-term Government of Canada bonds was 7.36 percent. However, the standard deviation was 9.01 percent, suggesting an average effective real rate of return that could fluctuate between -1.65 percent and 16.37 percent. This suggests that the plaintiff will almost certainly earn a rate of return different from the average long-term rate. Further, while a “profit” can be made by selling a bond when the interest rate decreases, a “loss” would occur if the interest rate increased (say) to six percent, where the 19-year bond would now only cost $33,051, for a net loss of $4,638 (or an effective rate of return of -12.31 percent).
Finally, if we were to rely on an average of past effective rates of interest then what period should we rely on? For example, the Canadian Institute of Actuaries report noted above indicates that the real effective rate of return on Government of Canada long-term bonds averaged -1.31 percent for the period 1956-1980, +8.74 percent for the period 1981-2005, and +6.79 percent for the period 2001-2005. There would be no justification for relying on any one of the above periods over the others, or for averaging these periods together, in attempting to obtain a forecast of the rate of return in the future.
We use the observed rates on government bonds as an indicator of the rates that are anticipated by large institutional investors, with billions of dollars at stake. While one might find that a forecaster is suggesting that (say) 3½ percent is the appropriate real long-term rate, this prediction is contradicted by the fact that the Government of Canada is presently able to sell its long-term bonds which offer a real return of less than three percent. (If expert institutional investors anticipated that real rates on secure investments will average, say 3½ percent over the next ten years, then they would not buy bonds that pay only 2½ percent, and the Government of Canada would be forced to adjust its bond rates.)
Other economists suggest that it would be simpler to assume that a plaintiff will hold a long-term security and then liquidate portions of this security to fund his/her losses in each year. This is simply another version of the market-based approach and, as discussed, there is a great amount of risk inherent in this strategy. Under our approach, if a plaintiff purchases a 5-year government bond with a value at maturity of $10,000, then in five years he is virtually guaranteed to receive $10,000 after redeeming his bond. However, if he were to buy a 20-year bond with the idea that he would liquidate portions of it to fund losses in each year, then he would be at the mercy of the bond prices available in each year. That is, he would be selling portions of his bond (as opposed to redeeming bonds for the guaranteed maturity value) and so, would be relying on the price of bonds attainable at the date he needed to fund his losses. As our discussion regarding the “conservative” versus “market-based” approaches illustrates, a plaintiff trying to fund his losses during periods of high interest rates would likely be selling portions of his bond at prices lower than his original purchase price and so, may not be able to fund his losses in each future year. If there is pressure on interest rates to increase in the next few years, as many economists feel is the case, then it is likely that plaintiffs investing awards from trials occurring in the next year or two would find themselves in this situation. We do not believe it is reasonable to impose this level of risk on a plaintiff.
Over the last ten years our prediction concerning the long-term interest rate has gradually declined from 4¼ percent to three percent. This decline has been in step with the observed rates, which can be seen in the above chart. Other economists have commented on our changes, with the implication that these changes demonstrate a weakness in our methodology. Our response is that the long-term rate has been changing over the past ten years, and it is important to reflect these changes in our calculations. To do otherwise would result in us using interest rates that are inconsistent with the rates that are actually available to plaintiffs.
Even if one finds that over the past few decades, long-term real interest rates have averaged 3½ percent, that rate is not now available to plaintiffs. Today’s plaintiff seeking secure investments simply cannot obtain a guaranteed long-term rate as high as the rates that were available 10 or 20 years ago. Even if the long-term rate rises to 3½ percent in five years, it does not follow that today’s plaintiff will be able to earn a long-term rate of 3½ percent, since he will be limited to the lower rates for the first five years.
Finally, many economists argue that plaintiffs should invest in equities, as well as bonds, and argue that this would result in a portfolio that is less volatile than investing in bonds alone. We find it difficult to justify the assertion that a portfolio that includes equities would be less volatile, given that the value at maturity of Government of Canada bonds is virtually guaranteed. Remember, the purpose behind the plaintiff’s investment of an award is to fund his losses in each future year and this is much different from investing for (say) retirement. The plaintiff must be able to fund his future losses in each year, whereas retirement can be delayed (or retirement plans changed) if there are insufficient funds. A plaintiff who invests in a series of bonds that provide the amount needed to fund his loss in each year, will receive the necessary amount with little to no risk of default. The same can not be said of equities, which carry a very real risk of default. The inclusion of equities can only increase the risk that a plaintiff will not be able to fund their future losses in each year.
We will re-examine our assumptions next year, and expect that some minor adjustments in our shorter-term rates may be warranted, depending on the movement of rates between now and then. As noted, minor changes in our assumptions regarding short-term interest rates will typically lead to negligible changes to our present value estimates. The assumed longer-term rates have a greater influence on our calculations, and if the rate on long-term bonds remains significantly below three percent (as it has since 2004), it may be appropriate to adjust our long-term rates as well.
![]()
