This article first appeared in the spring 2008 issue of the Expert Witness.
In estimating a plaintiff’s without- or with-incident income, there is a mathematical mistake that an economist can make that will potentially have a large impact on the resulting income path and, subsequently, on the plaintiff’s loss of income. This mistake is the practice of averaging multiple statistical sources together to obtain one “overall average”. It may seem reasonable, at first glance, to assume that averaging multiple sources of statistical data would result in an overall average which is superior to the quality of the individual averages. However, this is often not the case. This approach can lead to an incorrect and misleading estimate of a plaintiff’s income due to double-counting, a failure to take into account differing quality of each source (as measured by sample size), and the inclusion of important characteristics (such as age, education, and gender) that are not applicable to the plaintiff. This method also has the potential to provide misleading estimates simply based on the choice of the sources used in calculating this “average”.
To illustrate these effects, we have summarized in the table below, the average income for partsmen (as an example) obtained from a number of common statistical data sources.
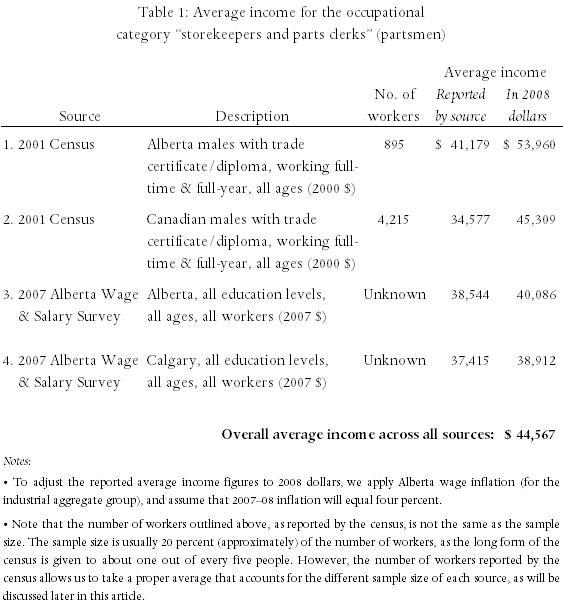
As shown in the table, if we were to “average” across all of the incomes then we would get an income figure of $44,567 (in 2008 dollars). However, this would be an incorrect and potentially misleading estimate of the average income of partsmen.
The first reason the above “average” figure is incorrect stems from a form of double-counting. Notice that sources one and three provide the average income of partsmen in Alberta, source two provides the average in the whole of Canada, and source four provides the average income of partsmen in Calgary. However, the Alberta data from source one are already included in the Canadian data from source two. Similarly, the Calgary data from source four are already included in the Alberta data from source three. Thus, the average incomes reported by sources one and four are based on data that were already present in sources two and three. Additionally, because the data from sources one and four are already included in sources two and three, these sources have been included in the overall average figure twice. This double-counting is mathematically incorrect and can lead to biased estimates of a plaintiff’s income (i.e. estimates which are either higher or lower than the actual average income). For example, if we were to use only the sources for Alberta overall (and exclude the sources for Calgary and for Canada overall), we would obtain an average income of $47,023 (or approximately $2,456 more than the “overall” average). Thus, taking an average across multiple sources of statistical data will lead to double-counting, and thus to biased estimates of a plaintiff’s income, due to this overlapping of data from a variety of sources (i.e. data from Canada includes data from Alberta, which in turn includes data from Calgary).
The second reason that taking an average across all of the sources is incorrect is that we have not accounted for the “quality” of each source, measured in this case by the size of the sample upon which the average income from each source is based. For example, we have applied equal weight to source one, whose average income was obtained using data from a Statistics Canada survey of approximately 179 workers (about one-fifth of the reported “number of workers” figure), as to source two whose average income was obtained using data from about 843 workers (almost five times as many as source one). In addition, we have taken an average that includes sources whose sample size is unknown. As an example, and ignoring the “double-counting” problem for a moment, if we were to take a simple average of sources one and two, we would get an overall average of $49,635 (= [$53,960 + $45,309] ÷ 2). However, if we were to calculate a proper average that takes into account the different sample size of each source, we would get an average income of $46,824 (= $53,960 × 895 / 5,110 + $45,309 × 4,215 / 5,110), or approximately $2,810 less than the simple average. Thus, taking a simple average across multiple sources of statistical data will lead to biased estimates of the plaintiff’s income, due to a failure to account for varying sample sizes across the different statistical sources.
The third reason that taking an average across multiple sources of statistical data is incorrect is that this figure includes income data from partsmen of varying education levels and gender. That is, (setting aside the double-counting and sample size problems for a moment), sources one and two provide average incomes for males with a trade certificate/diploma, while sources three and four are comprised of data for partsmen of all education levels, as well as from data for both male and female partsmen. Essentially, each of these sources provides income data for individuals who are not comparable to each other (the “apples to oranges” problem).
For example, the “overall” average figure combines the average income of partsmen with trade certificates or diploma with partsmen of all education levels. The partsmen with formal post-secondary training in their field will be expected to earn more than partsmen of all educations, since the latter group will include some workers without formal training. Thus, including the all-educations categories will bias the overall average downward if we are attempting to estimate the average income of partsmen with formal post-secondary training in their occupation. (And similarly, if we are attempting to estimate the average income of partsmen without formal post-secondary training, then including categories one and/or two will bias the average upwards.) Additionally, by including sources three and four, we have included data from female partsmen and from partsmen with varying levels of education. Thus, by taking an average across all sources, we have incorporated a variety of important characteristics (such as location, education, and gender) which may not be applicable to the plaintiff and which could significantly bias the resulting estimate of the plaintiff’s income.
Finally, the approach of taking an average across multiple sources of statistical data has the potential for allowing estimates to be biased upwards, or downwards, simply by choosing the sources that are included in the average. For example, we have included the 2001 Census and the 2007 Alberta Wage and Salary Survey in Table 1 and obtained an “overall” average of $44,567. Suppose we also found one survey that indicated an average income for partsmen of $60,000 and one survey that indicated an average income of $35,000. If both of these new sources were included in the “overall” average (and ignoring the double-counting, sample-size, and characteristic problems for the moment), we would calculate a new average of $45,545, which is close to our original average. However, if we chose to only include the $60,000 survey, our new average would be $47,653. Alternatively, we would obtain an average income of $42,653 by only including the $35,000 survey. In other words, one could potentially obtain an estimate of a plaintiff’s income which is biased upwards, or downwards, by simply altering the selection of sources. The fact that this method is open to this potential form of abuse suggests that this approach should not be used.
In summary, taking an average across multiple sources of statistical data can lead to biased estimates of a plaintiff’s income due to the double-counting of data, the failure to take into account differing sample sizes, and the inclusion of important characteristics (such as geography, age, education, and gender) that are not applicable to the plaintiff. In addition, this approach has the potential for abuse in that the estimate of a plaintiff’s income can be biased upwards or downwards by the selection of the statistical sources used in the calculations. Note that it may be difficult to detect these problems if the sources have not been adequately described or if the reader is not familiar with the sources or methodology used in calculating the average. A better approach would be to rely on one, high quality, well justified data source (such as the Canadian census). This avoids the many problems associated with combining multiple sources and does not open the door to using various sources to obtain a higher or lower estimate of a plaintiff’s income.
![]()