Category: Fatal accident claims

Cross versus Sole Dependency in Fatal Accident Actions

Posted on By economica

by Christopher J. Bruce

When a spouse has been killed through the negligence of a third party, the surviving spouse is entitled to damages that would allow him/her to maintain the standard of living that he/she had previously enjoyed.

The determination of this value requires that three steps be taken. First, the potential earning capacity of each spouse must be estimated. Second, a calculation must be made of each spouse’s dependency rate – that is, the percentage of family income that benefitted that spouse. Third, it must be determined whether any monies that had been spent on the deceased by the survivor (and which now do not have to be spent due to the death of the former) should be deducted from the survivor’s loss of dependency. In what is known as the sole dependency approach, that “saving” is not deducted. In the cross dependency approach, the saving is deducted.

In this article, I will use a concept that is fundamental to economic analysis – the rational person assumption – to suggest that basic economic principles favour the use of sole dependency.

I begin by making some simple assumptions about a couples’ earning capacity and dependency rates and use those assumptions to define sole and cross dependency. I then introduce the rational person assumption and provide examples of the use of that assumption in non-fatal accident cases. Finally, I extend the analysis to fatal accident cases and argue the rational person assumption provides support for use of the sole dependency approach.

Assumptions concerning earning capacity and dependency

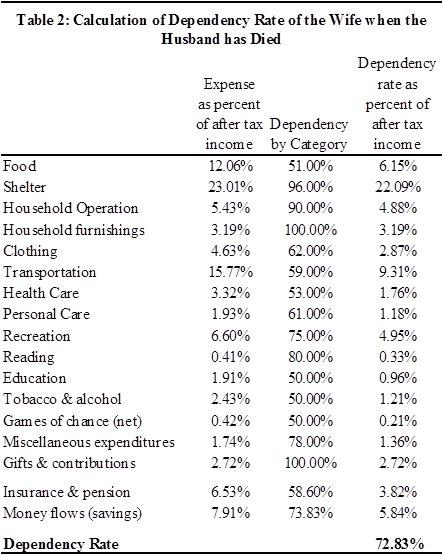
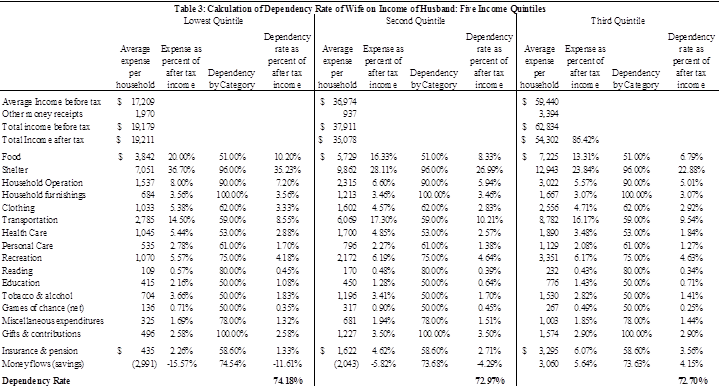
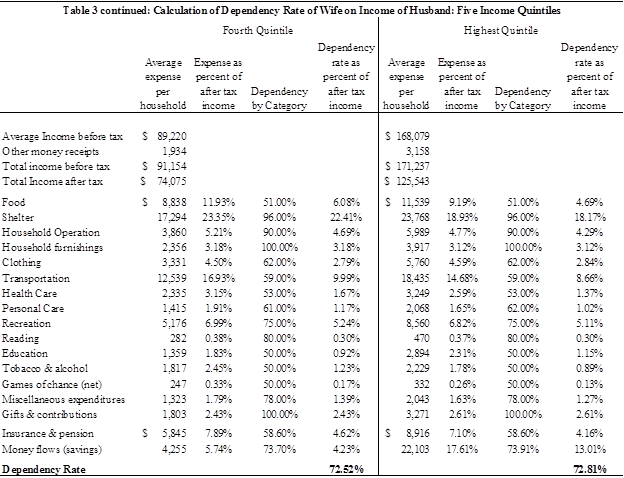
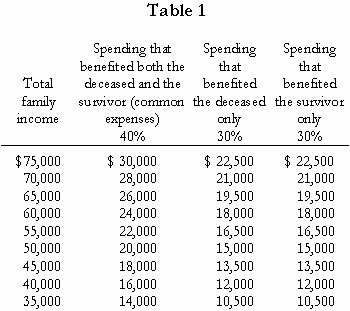
Statistical analyses suggest that, in a household consisting of a husband and wife, approximately 30 percent of the family’s after-tax income is spent on items such as food, clothing, and transportation that benefit the husband alone; approximately 30 percent is spent on items that benefit the wife alone; and 40 percent is spent on items, such as housing, furniture, and insurance, that benefit both spouses collectively. Each spouse benefits, in total, from 70 percent of family income – 30 percent that benefits that spouse personally – usually referred to as “personal expenses” – and 40 percent that benefits both spouses equally – “common expenses.” The 70 percent figure in this example is known as the individual spouse’s “dependency rate.” [Note that, as both spouses have the same dependency rate, 70 percent, there is a net benefit from marriage.]

Assume that in a childless couple, the husband earns $100,000 per year after taxes and the wife earns $40,000. Based on my assumptions concerning dependency rates, out of the husband’s income, 30 percent, or $30,000, is devoted to his personal expenses, 30 percent, or $30,000, is devoted to his wife’s personal expenses, and 40 percent, or $40,000, to common expenses. From the wife’s income, the comparable figures are 30 percent ($12,000), 30 percent ($12,000), and 40 percent ($16,000), respectively.

Cross and sole dependency defined

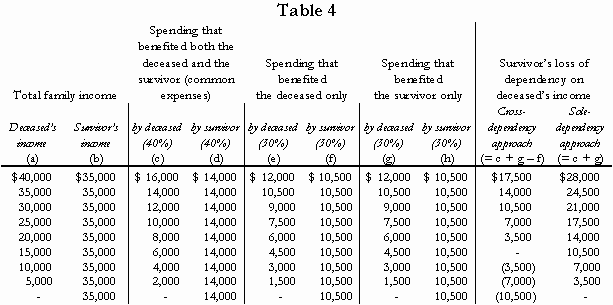
Now, assume that the wife has been killed. The sole dependency approach asks: how much of the wife’s future income would have been devoted to expenses that benefitted the husband? The answer in this case is that it is the 30 percent of her income that she spent on items specific to her husband (food, clothing, etc.) plus the 40 percent of her income that she spent on common expenses (housing, furniture, etc.), or $28,000 – which equals the husband’s dependency rate, 70 percent, multiplied by the wife’s (after-tax) income, $40,000. The tortfeasor would be required to pay $28,000 per year until the projected date of the wife’s retirement, discounted to the present.

Proponents of the cross dependency would also calculate the husband’s dependency on the wife’s income, here $28,000. But they would then argue that there is an offset against that loss: the “savings” obtained by the husband because he no longer devotes 30 percent of his income to his wife’s personal expenses. In the example here, as the husband was spending 30 percent of his income on his wife, it is argued that he now benefits from a $30,000 saving as a result of her death. The difference between this $30,000 saving and the $28,000 he has lost, $2,000 per year in total, represents a net benefit to him. He has no claim (for dependency loss) against the tortfeasor.

The “Rational Person” assumption

Which of these approaches is more consistent with the legal principal that plaintiffs are to be returned to the position they would have been in had the negligent action not occurred, restitutio in integrum?

When answering this question, economists rely on an assumption that is fundamental to economic analysis: that individuals act rationally to improve their own welfare. This rational person assumption implies that informed individuals will voluntarily undertake actions only if those actions make them better off (or, at least, no worse off). [Note the similarity to the “reasonable person” doctrine of tort law and to the rationale, in contract law, for maintaining the sanctity of contracts.]

As a simple example of the rational person assumption, assume that individual B is observed to be saving towards the purchase of a lap-top computer. One day, B sees an ad for the computer he likes, at a price of $1,000 (inclusive of all taxes). He checks his bank balance and discovers that he has $1,500. Assume we also observe him use his debit card to buy the desired computer; and, when he gets home, to check his bank balance again, to find that he now has $500.

Can we, as an external observer (with no ability to read B’s mind) conclude that B is “better off?” Economists, employing the “rational person” assumption, argue that B must be better off than if the purchase had not been made: a rational individual will only pay $1,000 for an item if he or she values that item at more than (or equal to) $1,000.

Although it might be argued that B is “worse off” in the sense that he now has $1,000 less than he would have had, that reduction in his finances is at least offset by the fact that he now has a computer that he valued at $1,000 or more.

To put it another way, if an individual was observed to go shopping with the intention of paying $1,000 for a computer, but was prevented from doing so because the store had run out of stock, no professional economist would argue that that individual was now “better off” — because he now has $1,000 that he would otherwise not have had. He is not better off. His preference was observed to be to trade the $1,000 for a computer – that would have made him better off. [Indeed, the rational person assumption suggests that when he is prevented from spending his money the way that he prefers, he is made worse off.]

The Rational Person argument applied to personal injury cases

Before examining how this view of rational behaviour applies to fatal accident cases involving spouses, I first turn to two other classes of tort actions.

In the first of these actions, assume that an individual has been seriously injured in a motor vehicle accident. As a result of this accident, her earning capacity has been impaired to the extent that she will lose $100,000 between now and the time she would have retired. The defendant accepts responsibility for this loss, but counters that offset against this loss is a “gain” that the plaintiff has obtained because of the accident. Imagine that before the plaintiff was injured, she was an active golfer, spending $5,000 a year on green fees, lessons, and equipment. The injuries suffered in the accident, however, are such that she can no longer play golf, thereby “saving” $5,000 per year. Assume also that evidence has been led to suggest that she would have played golf for another 25 years, had she not been injured. Hence, because of her injuries, she will save approximately $125,000 over her lifetime that would otherwise have been spent on golf. The defendant argues that when this saving is deducted from the plaintiff’s lost earnings, the plaintiff is actually $25,000 better off as a result of the accident. The defendant owes nothing to the plaintiff.

Using the assumption of the rational individual, however, it is easily seen why the defendant’s argument in this case is fallacious. Although it is true that the plaintiff will now have $125,000 available to her that she would not have had in the absence of the accident, she now has been denied $125,000 worth of pleasure that golf would have given her. Ignoring the effect of the accident on her earnings, in order for the plaintiff to be left in the same position she would have been in the absence of the accident, she will have to spend sufficient money to replace the value she would have obtained from golf. But this must be at least $125,000: because she would have chosen to spend $5,000 per year on golf in preference to spending it on anything else, $5,000 spent on “anything else” must be of lesser value than that expenditure on golf. That the plaintiff now has $125,000 that she would not have had if she had been allowed to spend it on golf does not make her $125,000 better off. At best, it leaves her in approximately the same position as she would have been in had she been allowed to spend that money. Hence, it is incorrect to suggest that the $125,000 that has been “saved” should be set off against the plaintiff’s loss of earnings.

In the second example of a tort action, assume again that the injuries suffered by the plaintiff in an automobile accident have reduced his lifetime earnings by $100,000. Again, the defendant has accepted responsibility for the accident; but in this case, she argues that as the plaintiff’s daughter was killed in that accident, the plaintiff has been “saved” the costs of raising that child. If those costs have been calculated to be $150,000 over the life expectancy of the child, the defendant argues that the net effect of the accident has been to leave the plaintiff no worse off than he had been in the absence of the accident. There is no loss.

Again, the fallacy of this argument arises because the defendant has implicitly argued that the plaintiff would not have received any benefit from the $150,000 he would have spent on his daughter. But, according to the “rational consumer” assumption, if the plaintiff had chosen to have the daughter and to spend $150,000 on her, in preference to spending that money in any other way, the plaintiff is worse off having $150,000 than he would have been spending that money on his daughter.

The Rational Person argument applied to fatal accident cases

With these cases in mind, consider again the case discussed at the beginning of this article, concerning the death of a wife. It is now seen that when the defendant argues that the cross dependency approach should be applied, what he is actually arguing is that the $30,000 the plaintiff had been spending on his wife had provided him with no benefit at all. Now that those expenditures have been “freed up”, he can spend the money on himself, at a net gain of $30,000. Therefore, the defendant argues that that gain can be set against other losses from the accident – as was argued by the defendants in the cases of the plaintiffs who were asked to set their savings of expenditures on golf or on their child against their losses of income.

But, as in those cases, the rational person assumption suggests that surviving spouses are not better off when they do not “have to” make expenditures on their deceased partners. If they were making those expenditures voluntarily (i.e. rationally), they must have obtained some benefit from that expenditure – indeed, a benefit that exceeded the value from any other purchases that could have been made with the same amount of money. Now that the husband in the example does not “have to” spend $30,000 per year on his wife, he can spend it on himself – clothes, travel, cars, etc. But does that expenditure give him as much pleasure as spending it on his wife? The better argument, I suggest, is that preventing plaintiffs from spending money in the way that they would have chosen cannot make them better off. Hence, it would be inappropriate to deduct any such purported “gains” from plaintiffs ‘other losses.

It is the sole dependency approach that is more consistent with both restitutio in integrum and with the rational person assumption.

Summary

A fundamental assumption in economics is that individuals are rational; and, therefore, that when an individual is observed to make a voluntary choice, it can be concluded that the individual must have expected that choice to make him/her better off (or, at least, no worse off). With respect to fatal accident actions, this implies that if spouses are rational, they must have expected that the decisions they made about spending on one another would make them better off. In this article, I have argued that if this proposition is accepted, the sole dependency approach is preferred to cross dependency.

 

Christopher Bruce is the President of Economica and a Professor of Economics at the University of Calgary. He is also the author of Assessment of Personal Injury Damages (Butterworths, 2004).

The Dependency Rate as a Percentage of After-tax Income: Canada 2008

Posted on By economica

by Christopher J. Bruce and Kelly A. Rathje

In fatal accident litigation, the plaintiffs are entitled to claim an amount that is sufficient to allow them to maintain the same standard of living as they had enjoyed when the deceased had been alive. In practice, this requires that the court calculate the percentage of the deceased’s  after tax income that would have benefited the survivors directly. In Canada, this percentage is called the dependency rate.

Although most experts conclude that the dependency rate of one member of a couple is approximately 70 percent of the deceased spouse’s (after tax) income; there has recently been some confusion over whether the dependency rate might increase or decrease as family income increases. In particular, some experts have argued that the survivor’s dependency decreases as the deceased’s income increases. For example, whereas the widow of a man with low income might need, say, 80 percent of his income in order to be left in the same financial state as she would have had he lived, the widow of a wealthy man might need only 50 percent.

The purpose of this article is to employ a reliable source concerning  after tax income, expenditure patterns, and savings – the Canadian Survey of Household Spending (SHS) – to investigate this claim. Based on the SHS, we show that the survivor’s dependency rate, in a husband/wife family, does not deviate significantly from 72 percent, regardless of the family’s level of income.

The article is divided into three sections. In the first, we argue that the Canadian data are reliable. Second, we calculate the dependency rate for a surviving wife at each of the five income quintiles. There we will show that that rate does not differ significantly from 72 percent at any of these quintiles. Finally, we comment on the treatment of savings in the calculation of the dependency rate.

We also include an Appendix in which we calculate a dependency rate by category for each of the 17 categories of expenditure in the SHS. [Note: in this article, we do not comment on the question of whether some portion of the survivor’s incomes – the portion they now “save” because they do not “have to” spend it on the deceased – should be set off against the survivor’s loss. The arguments we make here apply equally to both the set-off, or cross-dependency, and sole-dependency approaches.]

I. Survey of Household Spending

The most reliable source of family expenditure data in Canada is Statistics Canada’s Survey of Household Spending (SHS), in which approximately 15,000 families are interviewed. The most recent such survey (for which appropriate data are available) was conducted in 2008. The primary source of information concerning this survey is Statistics Canada’s Spending Patterns in Canada, 2008 (Catalogue No. 62-202-XWE).

The 2008 SHS breaks down gross family income into 18 components: 15 major categories on current expenditures, two categories that reflect future expenditure – “insurance and pension contributions” and “money flows” (where the latter is a measure of net savings) – and one for income taxes. Summary information is provided concerning: number of families in the sample, average family size, number of adults, children, and age of head.

Table 1 provides an example of the type of information that can be drawn from the 2008 SHS. The first column in this table reports the average annual expenditures on each of 17 categories (other than taxes). The second column reports the percentages of total (after tax) income that were devoted to each of these categories.

There are a number of reasons for believing that the SHS data are reliable. First, Statistics Canada makes an effort to collect information from the family head. Second, the data for recurring expenses, such as food and personal care, are collected using a detailed daily diary. Third, all other data are collected through personal interviews taking two to three hours. Finally, Statistics Canada has confirmed that the average incomes reported by respondents to the SHS are consistent with those collected from other sources (such as income tax data) 1.

II. Dependency Rates by Income Quintile

The Appendix to this paper calculates the dependency rate for each of the 17 categories reported in Table 1. This rate is the percentage of the pre-accident expenditures on that category that the surviving spouse will need in order to maintain his or her pre-accident standard of living.

These dependency rates are reported in the second column of Table 2. The rate for each category has been multiplied by the percentage of current consumption devoted to that category, taken from the first column of Table 1, in order to obtain the figures reported in the third column. The latter represent the percentages of pre-accident,  after tax income that the surviving wife will need in order to maintain her pre-accident standard of living.

For example, the first row of Table 2 reports that the average Canadian family spent 12.06 percent of its after tax income on food, and that a widow will need 51 percent of this figure to maintain her pre-accident standard of living. Hence, she now needs 6.15 percent (= 0.51 × 12.06) of the family’s pre-accident income in order to purchase the food that she would have purchased had her husband not been killed.

When similar calculations are made for each of the 17 categories reported in Table 2, and the resulting figures are summed, it is found that the wife will require 72.83 percent of after tax income to maintain her pre-accident standard of living.

Using the same methodology employed to obtain the dependency rate for the average family, we also calculate dependency rates for families in each of the five income quintiles. In Table 3 (shown on the next two pages due to size constraints), we report the findings for each of these calculations, plus data concerning: the incomes of each of these groups and the distribution of their expenses among the 17 expenditure categories.

It is seen there that, before taxes, household incomes vary from a low of $19,179 for the first quintile to a high of $171,237 for the fifth; that income taxes range from 3.44 percent to 24.89 percent of total income; and that savings (as measured by the “money flow” category) range from minus 15.57 percent to plus 17.61 percent of  after tax income.

The most compelling finding in Table 3 is that dependency rates do not vary significantly with gross income, with figures ranging from a low of 72.52 percent for the fourth quintile to a high of 74.18 percent for the first quintile 2. Although this finding may, at first, seem counterintuitive, three factors help to explain it.

First, it is seen in Table 3 that the distribution of expenditures among categories does not vary appreciably among income groups. For example, even in the category with the greatest difference among income groups, shelter, families in the fifth quintile spend only nine percentage points more than do families in the second quintile (28.11 percent versus 18.93 percent). In no other category does percentage expenditure decrease or increase by as much as seven points between the second and fifth quintiles.

Second, because the percentages of expenditures on the 17 categories have to add to 100 percent, every increase in the fraction of income spent on one category must be offset by a decrease in the fraction spent on another. Thus, as long as the dependency rates of the categories that increase are similar to those of the categories that decrease, the average dependency rate across categories will not change.

Finally, our finding that dependency rates do not vary significantly with income depends in part on the assumption that the survivor’s dependency on savings will be the same as her dependency on current consumption – that is, on the assumption that, to maintain her standard of living, the survivor will need the same percentage of the family’s retirement income as she needed of its current income.

If, however, the survivor could only be “made whole” if she was allocated a higher (or lower) percentage of retirement income than current income, then dependency rates would increase (or decrease) as income rose – because high income families devote a higher percentage of their incomes to savings. We discuss this issue in greater detail in Section III.

III. Dependency on Savings

Assume that a husband and wife have family income of $80,000 per year, after taxes, of which they devote $70,000 to current expenditures (that is, to expenditures on food, clothing, shelter, etc.) and $10,000 to savings. Assume also that the wife’s dependency on current expenditures is 70 percent – that is, that she benefits from $49,000 (= 0.70 × $70,000) worth of goods and services each year (during the years in which her husband is working). If her husband is killed, she will require replacement of that $49,000 if her standard of living is to be maintained.

In addition, her husband’s death will deprive her of the benefit she would have received from the (ultimate) expenditure of the $10,000 per year that the couple was saving. In Section II, we assumed that the couple would have spent that money in a manner that was similar to the way in which they were spending their income on current expenditures. Therefore, we would have applied a dependency rate of 70 percent to the $10,000 to determine the loss to the wife.

It appears to us that there are two arguments against use of the latter assumption. First, it may be that, as retired couples have lower incomes than working-age couples, their expenditure patterns will also differ, resulting in different dependency rates. However, as we have found that dependency rates do not vary significantly across income levels (see Section II), this argument is not likely to have a significant effect on the results in Table 3.

Second, it is possible that couples may intend to leave a large portion of their savings either to charity or to their children.

To the extent that charitable donations and bequests are a “public good,” the surviving spouse may need as much as 100 percent of planned donations if she is to maintain her standard of living. For example, if the couple had planned to give $100,000 to their daughter, the surviving wife will not be left “equally well off” if the death of her husband leaves her able to give some amount less than $100,0003.

Assume, for example, that within the highest quintile, couples plan to spend 60 percent of their savings on the purchase of goods and services (when retired), and 40 percent on donations and bequests. If it is assumed that the wife’s dependency on current expenditures is 70 percent and her “dependency” on donations and bequests is 100 percent, her total dependency on savings will be 82 percent (= 0.60 × 70% + 0.40 × 100%), instead of the 73.91 percent we applied to savings in Table 3. In that case, however, her total dependency on after-tax income would increase by less than 1.5 percentage points.

Furthermore, this argument has almost no effect on the dependency rates for couples in the first four quintiles as their savings rates are either very low or negative (implying very small donations and bequests). Thus, once again, adjustment of the assumption concerning dependency on savings has no significant effect on the general conclusion that dependency rates do not vary appreciably with income.

APPENDIX: Dependency Rate by Expenditure Category

The purpose of this Appendix is to calculate the dependency rates for each of the seventeen expenditure categories identified in the Survey of Household Spending.

a) Food: Two steps must be taken in order to determine the dependency with respect to expenditures on food. First, it is necessary to identify the relative consumption levels among family members of different ages and sex. Second, allowance must be made for the fact that economies of scale from bulk buying are lost when one member is removed from the family.

With respect to the first of these calculations, our research indicates that the relative consumption of food, among family members of different ages, can be approximated by the figures in our Table A.1.

For example, if a family is composed of a husband and wife, for every 1.0 “units” of food consumed by the husband, the wife consumes 0.8 units. In this case, the couple consumed 1.8 units of food, of which 44.4 percent (0.8 ÷ 1.8) was devoted to the wife. It is this figure that has been used in the construction of Table 2.

Based on the above, and on the general finding that food costs approximately 10 percent more for a single person than for each member of a married couple due to loss of economies of scale, we conclude that in a family of two adults the dependency would be 51 percent when it is the husband who has died and 61 percent when it is the wife. In a family of four, the dependency would be approximately 76 percent if the husband should die and 83 percent if the wife should die.

b) Shelter: The shelter category consists primarily of payments for rent, mortgage, repairs and maintenance, and utilities, none of which could be expected to be reduced appreciably following the death of a spouse. For this reason, we recommend that the dependency be set at 96 percent. This is the figure that has been entered the second row of Table 2.

c) Household operation: This category consists, principally, of expenses for telephone, child care, domestic services, pet care, household cleaning supplies, paper supplies (e.g., toilet paper and garbage bags), and gardening supplies. Of these, only expenses on telephone and paper products can be expected to vary appreciably with family size. Accordingly, we set the dependency rate at 90 percent for the childless family.

d) Household furnishings: As there is no element of this category on which expenditures would be reduced by the death of a spouse, the dependency is 100 percent.

e) Clothing: The most reliable source of data concerning the division of clothing expenditures among family members is Statistics Canada’s Family Expenditure Survey, 1986. Relying upon that source, we have calculated that a family of two adults and two children (aged five to nine) would require approximately 0.6 adult male units for the boy’s clothing, 0.8 for the girl’s clothing, 1.65 for the wife’s clothing, and 1.00 for the husband’s. Thus, the dependency would be approximately (3.03 ÷ 4.05 =) 75 percent if the husband should die and (2.40 ÷ 4.05 =) 59 percent if the wife should die. In a family of two adults, the equivalent dependencies would be 62 and 38 percent, respectively.

f) Transportation: Approximately 90 percent of transportation is devoted to the purchase, maintenance, and operation of cars and trucks. Thus, the most important determinant of the dependency in this respect will be the number of vehicles owned by the family. If both adults drive but own only one car, the death of one of them can be expected to have little effect on vehicle costs; that is, the dependency would be relatively high.  However, if the family owned more than one vehicle, including one that was used primarily by the deceased, the dependency may be as low as 50 or 60 percent.

For the purposes of illustration, we have assumed in the construction of Table 2 that the family had two cars, giving it a dependency with respect to vehicles of approximately 60 percent. The remaining 10 percent of the transportation budget is devoted to public transportation (including air fares).

Assuming that these expenditures are divided evenly among family members, the total dependency with respect to transportation is 62 percent (= [0.9 × 0.6] + [0.1 × 0.75]) for a four-person family and 59 percent (= [0.9 × 0.6] + [0.1 × 0.50]) for a two person family.

g) Health care: Approximately 30 percent of this expenditure is devoted to health insurance. As premiums generally do not double when family size is increased from one to two, we assume for purposes of illustration that the dependency with respect to health insurance premiums is 60 percent for a two-person family. The remaining 70 percent of the average family’s medical budget is devoted primarily to eye care, dental care, and drug purchases. Lacking any firm data on the distribution of these expenses within the family we shall, for purposes of illustration, assume that they are divided equally. Thus dependency for a two-person family is 53 percent (= [0.30 × 0.6] + [0.70 × 0.5]).

h) Personal care: Personal care includes expenditures on such items as haircuts, hair and makeup preparations, soaps, deodorants, and shaving preparations. The recommended budget developed by the Social Planning Council of Toronto shows that adult females spend approximately 63 percent more than adult males on these expenditures. Hence, if it is the husband who has died, the wife’s dependency is approximately 61 percent.

i) Recreation: Approximately 50 percent of the average family’s recreation budget is devoted to expenditures that may not vary with the size of the family, such as purchases of recreational vehicles and home entertainment equipment. The remaining 50 percent is devoted to admissions to events, purchases of home recreational equipment (such as games and crafts), and purchases of sport and athletic equipment. Assuming that the latter expenses are shared equally among family members, the dependency with respect to recreation proves to be 75 percent (= [0.5 × 1.0] + [0.5 × 0.5]) for a two-person family.

j) Reading: The approximate division of reading is: 35 percent on newspapers, 20 percent on magazines, and 45 percent on books. Assuming that newspaper expenses do not vary by size of family and that one-third of book and magazine purchases are specific to one of the adult members of the family, the dependency with respect to reading proves to be approximately 80 percent (= [0.35 × 1.0] + [0.65 × 0.67]).

k) Education: In the absence of any information concerning the plaintiff family, and recognizing that less than 20 percent of the education expenses listed by Statistics Canada are devoted specifically to young children, the only assumption that can be made with respect to this category is that expenses are divided equally between the two adults if there are no older children in the family. That is, for purposes of Table 2, the dependency is 50 percent.

l) Tobacco and alcohol: As with education, in the absence of specific information about the family and assuming that there are no older children in the family, the dependency for tobacco and alcohol must be set at 50 percent.

m) Games of chance: In the absence of other information, we assume that the couple divides these expenditures equally. That is, the dependency rate with respect to this category is 50 percent.

n) Miscellaneous: Of the expenses listed under Miscellaneous, approximately 70 percent reflect items that would not vary significantly with family size, such as interest on personal loans, purchases of lottery tickets, bank charges, lawyers’ fees, and funeral expenses. Assuming that the dependency with respect to these items is 90 percent and with respect to the remaining items is 50 percent, the total dependency with respect to the miscellaneous category is 78 percent (= [0.7 × 0.9] + [0.3 × 0.5]).

o) Personal insurance payments and pension contributions: Approximately 70 percent of the expenditures in this category are for pension fund payments (primarily the mandatory, government-operated Canada Pension Plan), 15 percent for life insurance premiums, and 15 percent for employment insurance premiums. Thus, the value of the dependency will be determined primarily by the labour force attachments of the adult members of the family and by the number and ages of children.

Consider, first, the life insurance premiums. In a two-adult family, life insurance is normally taken out on the life of the main income earner, with the second family member being the beneficiary.  If either family member dies, the need for such insurance is reduced significantly. That is, the dependency is (approximately) zero.

In a family with children, however, it may be the children who are made the beneficiaries.  Therefore, regardless of which parent has died, the remaining parent can be expected to continue his or her payments to a life insurance scheme.  Indeed, that parent may even increase life insurance coverage to take account of the fact that a further death would leave the children with no parents. In such a case, a 100 percent dependency would appear reasonable.

The value of the dependency with respect to employment insurance contributions will be determined by the employment status of the adult members of the family.  If the deceased was employed and the survivor is not, no contributions will now have to be made to employment insurance.  Therefore, the dependency is zero.  On the other hand, if the deceased was not employed and the survivor is, contributions will be unaffected.  That is, the dependency is 100 percent. And if both adults were fully employed, the dependency will be 50 percent.

Finally, when the family loses the deceased’s contributions to a pension plan, it loses the future consumption it would have enjoyed from that pension. As it is only the spouse, and not the children, who would have benefited from this pension, it is the surviving spouse’s dependency on the couple’s retirement level income that will be relevant.

Applying the technique described in Section II, above, we find that if both members of a couple are over 65, the surviving spouse will have a dependency rate of approximately 73 percent (whether it is the wife or the husband that has died). Hence, if both spouses had been fully employed, the total dependency on the personal insurance and pension contributions category becomes 73.6 percent (= [0.15 × 1.0] + [0.15 × 0.5] + [0.70 × 0.73]) when there are children and 58.6 percent (= [0.15 × 0] + [0.15 × 0.5] + [0.70 × 0.73]) when there are not.

p) Gifts of money and contributions: This category consists of gifts to individuals outside of the family-spending unit – for example to parents and children living in separate households – and of charitable donations. We believe it can be argued that if the wellbeing of the survivors is to be maintained at the pre-accident level, these contributions must also be maintained at the pre-accident level. That is, the dependency with respect to this category is 100 percent.

q) Money flows – assets, loans and other debts: The purpose of this category is to measure households’ net contributions to (or withdrawals from) savings. Its primary components are changes in bank balances, purchases of stocks and bonds, contributions to registered retirement savings plans, and changes in money owed by (or to) the household. To the extent that any money put in to savings will be spent later, the dependency on this category will be the same as the dependency on expenditures that were made while the family members were working, or approximately 74 percent, (see Section II). However, if a significant portion of the household’s financial assets are passed to the couple’s children, through their estate, the dependency on savings approaches 100 percent (as for “gifts and contributions”). For the purposes of the sample calculations reported in Section II, we have assumed that the couple spends all of their savings during their lifetimes. Accordingly, we employ a dependency rate equal to the dependency on current consumption, or approximately 74 percent.

Footnotes:

  1. Personal interview with Danielle Zietsma, Senior Economist, Survey of Household Spending, Statistics Canada, May 31, 2013. [back to text of article]
  1. We repeated the exercise in Table 3 using data for the situation in which it is the wife that had died. The dependency rates for the five quintiles did not change appreciably. They became 74.07%, 72.63%, 71.95%, 71.57%, and 71.56%, from lowest to highest quintile.[back to text of article]
  1. In Ratansi v. Abery (1994), 97 B.C.L.R. (2d) 74 (S.C.) the deceased parents had contributed a substantial portion of their income to their mosque. The court found that it was not “….appropriate or accurate to describe the monies contributed to that institution as ‘income not available for family expenditure’.” Accordingly, the dependency of the surviving children on this portion of their parents’ income was found to be 100 percent.[back to text of article]

leaf

Christopher Bruce is the President of Economica and a Professor of Economics at the University of Calgary. He is also the author of Assessment of Personal Injury Damages (Butterworths, 2004).

Kelly Rathje is a consultant with Economica and has a Master of Arts degree (in economics) from the University of Calgary.

Fatal Accident Calculations Under the New Legislation

Posted on By economica

by Kelly Rathje

This article first appeared in the autumn 2007 issue of the Expert Witness.

Recent changes to the Insurance Act in Alberta (amendment R.S.A. 2000, c. 1-3 defined in section 626.1) may affect the treatment of survivor pension benefits in fatal accident calculations. Prior to the legislative change, survivor pension benefits were treated as a collateral benefit – in the sense that they represented insurance proceeds paid for by the deceased’s CPP contributions – and these benefits were not included when estimating the family’s dependency loss. Any deduction for the survivor’s benefit would have been equivalent to reducing a loss of income-dependency award because the survivor had received some life-insurance proceeds.

Under the new legislation, however, the forms of payment to be deducted from the award include:

(d) benefits under a prescribed income continuation or replacement plan or scheme…

Thus, under the new legislation, it may be argued that for fatal accidents occurring on or after January 26, 2004, any survivor benefits should now be deducted from the loss of dependency award as these represent “income continuation or replacement”. However, note that the Act does not specifically address CPP survivor’s benefits, though it does state that CPP disability pensions are to be deducted from an injured plaintiff’s losses. It may be argued that the same reasoning applies in the case of a fatal accident, and the survivor’s pensions will be found to be deductible.

Note that this may also imply that any private pension benefits that are received by a surviving spouse may also need to be included in the dependency loss calculations. For example, if the deceased was a teacher or nurse, presumably the surviving spouse would receive any private pension contributions in the form of a lump-sum payment or monthly survivor pension benefits.

In light of the legislation change, we propose that since survivor benefits are now to be deducted from the dependency losses, they must also be factored into the without-accident income path. That is, in any given year there would have been a possibility that the deceased would have died and the survivors would have received benefits, (had the accident under litigation not occurred). In the past, we would not have considered these benefits to be “income” as they would have been treated as collateral benefits.

Allowing for these changes to the legislation requires that we take a two-step approach to estimating the deceased family’s loss of dependency on income.

In the first step, we undertake the following calculations to estimate the family’s loss of dependency.

  • We estimate the employment and retirement incomes that the deceased would have earned over his life, had the accident not occurred (his “without-accident” income path), and the probability that the family will experience a loss of dependency on that income.
  • We then estimate the survivor benefits that dependents would have received had the deceased died, and the probability that these benefits would have been received.
  • We multiply each year’s loss by the probability of each event occurring in the years following the accident, and add the resulting figures to estimate a stream of losses.
  • Finally, we calculate the present discounted value of the stream of losses.

In the second step, we calculate the present discounted value of the survivor benefits the family is now receiving. The dependency loss is then the difference between the figures calculated in the two steps – the expected value of the loss of dependency and the present value of the survivor benefits.

For the loss of dependency calculations, contingencies that reflect the probabilities that the couple might have eventually separated or that the surviving spouse may remarry, are also usually included. These contingencies have the effect of reducing the dependency loss. If the couple had separated, then presumably the surviving spouse would not have benefited from the deceased’s income, and if the surviving spouse remarries, then presumably he/she will no longer be dependent on the deceased’s income. However, when estimating the probability that the surviving spouse would have received survivor benefits regardless of the accident, we do not include remarriage contingencies. Had the deceased died regardless of the accident, the surviving spouse would have received survivor benefits as long as the couple had not separated by that time. Whether or not the spouse subsequently remarried would not have altered his/her eligibility for survivor benefits. Therefore, remarriage has no effect on the without-accident survivor benefits and does not need to be included in the calculations.

Potential issues

Collateral benefit

The argument that survivor benefits should be deducted from the loss of dependency award is based on the assumption that they represent “income continuation or replacement,” as specified in the new legislation. There is, however, an argument that survivor pensions should be treated as “proceeds from insurance,” not as “income continuation” benefits. If they fall in the former category, they may be considered to be a collateral benefit, which would not be deducted.

For example, suppose the surviving spouse is receiving a pension from a private plan. It may be argued that this pension is a collateral benefit – in the sense that it represents insurance proceeds paid for by the deceased’s acceptance of a reduced direct pension. Presumably the deceased had a choice between accepting a pension with a survivor’s benefit and a higher pension with no survivor’s benefit. Both pensions would be actuarially equivalent. The deceased’s choice of the “survivor’s benefit” option is effectively the same as if she had chosen the option of a higher pension with no survivor’s benefit, and used the additional income (while she was alive) to buy life insurance. Had she done so, it is our understanding that the life insurance proceeds would be considered to be a collateral benefit, and not deducted from any dependency losses. That is, any deduction for the survivor’s benefit would be essentially the same as reducing a loss of income-dependency award because the survivor has received some life-insurance proceeds. The courts do not allow the latter, as we understand the law.

Conservative estimate of survivor benefits without-accident

In our calculations, we assume that the survivor benefits actually received by the family are a reasonable reflection of the benefits they would have received had the deceased not died in the action under litigation. This is likely a conservative estimate that will understate the losses since the longer the deceased would have contributed to a pension plan, the higher the benefits would have been.

leaf

Kelly Rathje is a consultant with Economica and has a Master of Arts degree (in economics) from the University of Calgary.

Fatal Accident Dependency Calculations

Posted on By economica

by Derek Aldridge

This article was originally published in the winter 1999 issue of the Expert Witness.

We occasionally review cases in which the defendant is arguing that, after a fatal accident, the surviving spouse is financially better off. This sort of argument can be somewhat appealing in certain circumstances, but upon closer examination the “logic” is always unsupportable. Of course, I am referring to the distinction between sole- and cross-dependency. In this article I will briefly explain what dependency rates represent, and then offer a fairly detailed explanation of the differences between the sole-dependency approach and the cross-dependency approach.

Dependency rates are used to estimate a person’s financial loss due to the death of his or her spouse or parent. In a two-person household, if the husband dies, then the wife will no longer benefit from her husband’s income. However, she does not need to be compensated for the loss of all of his income, since some would have benefited him only.

To properly compensate the surviving dependant, it is necessary to determine how much of the deceased’s income the survivor needs in order to maintain the same standard of living as if the accident had not occurred. To make this determination, one must estimate how much of the deceased’s income would be allocated to common expenditures (mortgage payments, for example), and how much would be allocated to each spouse’s personal expenditures (food, clothing, and hobbies, for example). Our research suggests that, in general, about 40 percent of after-tax family income is allocated to common expenditures, and 30 percent to each spouse’s personal expenditures. We make the reasonable assumption that each spouse allocates his/her income in this manner. Thus, the surviving spouse requires approximately 70 percent of the deceased’s “without-accident” income, in order to maintain the without-accident standard of living. That is, the survivor still needs the 40 percent of the deceased’s income that would have been spent on common expenditures, as well as 30 percent that would have been spent on the survivor’s personal expenditures, but does not need the 30 percent of the deceased’s income that benefited the deceased only. The 70 percent is the dependency rate. Thus, I would argue that if the deceased would have earned $30,000 per year (after taxes and contingencies), had the accident not occurred, then the survivor now needs 70 percent of this income, or $21,000 per year in order to maintain the without-accident standard of living.

This approach – known as the sole dependency approach – is very appealing in many cases, thanks to its simplicity and the intuitively reasonable results that it generates. However, it is often argued that it needs to be modified in order not to over-compensate the survivor. The issue is how to treat the survivor’s income that would have benefited the deceased only. One might argue that the survivor’s lost share of the deceased’s income should be offset against her financial “gain” because she no longer spends money on items which benefited her husband exclusively. This is known as the cross-dependency approach.

I will attempt to more clearly explain the distinction between sole- and cross-dependency through a series of tables in which we consider a range of possible incomes earned by a hypothetical couple. (For the purposes of this article, I ignore the effect of dependent children.)

Table 1 illustrates how a couple’s income is allocated among the three broad expenditure categories, for a range of different income levels. (The reason why several different income levels are presented will become apparent later.)

Table 1

We can take the examples shown in Table 1 a step further by examining the more general case in which we consider the income earned by both members of the household. This is shown in Table 2. Note that the “total family income” figures in Table 2 are exactly the same as those in Table 1. As are the spending allocation figures.

Table 2

We can take this example another step further by considering how each member of the household allocates his/her income. Presumably, both spouses follow the 40/30/30 percent pattern when spending their income. Thus, each allocates about 40 percent of his/her income to common expenditures, 30 percent to his/her own personal expenditures, and 30 percent to the spouse’s personal expenditures. In Table 3 I follow the examples from Table 2, except that I show the allocation of spending by each spouse. Note that the “total family income” figures in Table 3 are exactly the same as in Tables 1 and 2, as are the totals of the individual spending allocation figures.

Table 3

Using the figures shown in Table 3, I can estimate the survivor’s financial loss upon the death of his or her spouse. It is clear that for the survivor to maintain the same standard of living as if the accident had not occurred, he or she will need enough income to fund the common expenditures shown (columns c & d), as well as the expenditures that were for his/her own personal benefit (columns g & h). Thus, what the survivor has lost, due to the death of his or her spouse is the sum of columns c and g. (The survivor has not lost columns d and h because he or she is still earning the income to pay for those expenses.) This is the sole-dependency approach.

The cross-dependency approach asks the question, “What should happen with the share of the survivor’s income that the survivor would have spent on the deceased (column f)?” The cross-dependency approach finds that this income has been saved, and should be offset against the sum of columns c and g. It finds that the survivor’s loss equals c + g – f. (Instead of just c + g, which is the finding of the sole-dependency approach.)*

Note that the dependency losses using either sole- or cross-dependency are always reported as the total of c + g – f (for cross-dependency) or the total of c + g (for sole-dependency). This is conventional, but it would be equally reasonable to report the individual components under separate heads of damage. For example, considering the top row of Table 3, the results could be reported as follows:

Results Table

With the total cross-dependency loss separated into its individual components (above), it is clearer why I disagree with that approach. First, I do not believe that it is economically correct to deduct the portion of the survivor’s income that would have been allocated to the deceased’s personal expenditures ($10,500) from the other components of the loss. Second, I do not believe that this deduction is consistent with other forms of personal injury damage assessment.

From an economic standpoint, I do not agree that the survivor’s income that would have been allocated to the deceased’s personal expenditures ($10,500 in the above example) should be deducted from the other components of the loss. I think most would agree that individuals spend part of their income on their spouses because they want to – in economic terms, they receive an offsetting benefit. Following the death of a spouse, the best that a survivor can do is spend this money on alternative goods. But, since the survivor had previously chosen to spend this money on his or her spouse rather than these alternative goods, these goods must represent a “second-best” choice. For example if a surviving wife had previously been spending $3,000 on goods which benefited her (now deceased) husband alone, and she now spends that money on alternative goods then, at best, that expenditure leaves her no better off than before. She has simply transferred the $3,000 from one set of expenditures to another. Hence, the $3,000 should not be offset against her loss of dependency.

It is my view that the correct way to compensate the survivor in this case is for the defendant to provide her with the income contribution that her husband would have made, had the accident not occurred (that is, the contributions to common expenses and to expenses which benefited the survivor only). The portion of the wife’s own income that would have been spent on her husband should remain available to be spent elsewhere at its second-best use (on holidays, gifts, charitable contributions, or whatever). From an economic standpoint, this will not leave the survivor financially better off. To argue in favour of cross-dependency, one must surely explain why the survivor is expected to use a portion of her own employment income to offset the defendant’s obligation.

I also do not believe that the deduction component of the cross-dependency approach is consistent with other forms of personal injury damage assessment. Cross-dependency requires that a plaintiff’s losses due to an accident should be reduced by any “savings” due to the accident (see the discussion above). Similar “savings” are seen in other forms of personal injury damage assessment, but are not deducted from losses. For example, plaintiffs who will be forced to retire early (or are unemployable) due to their injuries will “gain” a great deal of leisure time during the years when they otherwise would have worked. The value of this gain in leisure is not deducted from their losses. A father who was injured in a car accident that killed his son will now “save” the money he would have spent on his son. That savings is not deducted from the father’s loss of income award. Quadriplegics will “save” money on shoes, golf memberships, ski passes, and so forth. That savings is not deducted from their other losses.

Another difficulty with the cross-dependency approach is that if one follows the methodology consistently, it leads to indefensible results in many cases. Following the examples shown in the tables above, we see – below – that if the deceased’s income was much less than the survivor’s then cross-dependency will show that the survivor’s loss is negative (a net gain).

Table 4

As shown by the examples in Table 4 (above), the sole dependency approach yields results that are, intuitively, much more reasonable, given a wide range of income assumptions. The sole-dependency approach will never find that a survivor is financially “better off” following the death of his or her spouse. As shown, the cross-dependency approach will yield such a result in cases in which the deceased earned much less than the survivor.

The “negative loss” results generated by the cross-dependency approach are often ignored, and it is stated that the survivor has suffered “no net financial loss”. Of course the true result implied by the cross-dependency approach is that the survivor has experienced a net financial gain. Cross-dependency is always ignored when the deceased did not earn any income (and the survivor was the sole income earner), since the method – if followed – will always show that the survivor is financially better off. If the cross-dependency approach was accepted, it would seem that in such a case the survivor’s gain in net income should be offset against his or her loss of dependency on household services. Of course it is not. In my view, part of the reason why the cross-dependency approach has enjoyed some level of acceptance is because its supporters only use it when it yields results that seem intuitively reasonable. When cross-dependency leads to the nonsensical results described here, it is usually (if not always) abandoned.

Footnotes

* Note that the above description of cross-dependency is sometimes stated differently, although mathematically it is the same. The other way to describe cross-dependency is that it is 70 percent of the couple’s combined pre-accident income, less the survivor’s income. That is, 0.7[a + b] – b, using the above table. This is the same as 0.7a + 0.7b – b. Note also that 0.7a = c + g; 0.7b = d + h; and b = d + f + h. Thus the cross-dependency loss equals c + g + d + h – [d + f + h]. This reduces to c + g – f, which is exactly the same as I noted above. [back to text of article]

leaf

Derek Aldridge is a consultant with Economica and has a Master of Arts degree (in economics) from the University of Victoria.

Calculation of the Dependency Rate in Fatal Accident Actions

Posted on By economica

by Christopher Bruce

This article first appeared in the winter 1996 issue of the Expert Witness.

In a fatal accident action, the surviving spouse is entitled to claim for any loss of pecuniary advantage which would have been derived from the deceased. There is considerable uncertainty, however, concerning the manner in which this loss of dependency is to be calculated. The purpose of this paper is to discuss three alternative approaches to the calculation of the dependency and to argue that selection among them depends upon the nature of the couple’s marriage. The three approaches are defined in the first part of the paper. In the second, three types of marriage are defined and each type is matched with an associated method of calculating the dependency.

Theoretical Approaches to Calculation of Dependency

Assume that the husband of a childless couple has been killed. The husband was earning $30,000 per year (after taxes) and the wife $20,000 per year. Assume also that the wife’s dependency on family income has been found to be 70 percent – composed of 30 percent of family income spent on items which benefitted the wife alone and 40 percent spent on items which benefitted the husband and wife equally. Three different approaches to the calculation of the wife’s loss can be identified.

a) The sole dependency method

In this approach, the wife receives 70 percent of her husband’s projected income.

b) The “traditional” cross-dependency method

In this approach, the wife receives 70 percent of the family’s income net of her earnings:

(0.70 x $50,000) – $20,000 = $15,000 (2)

The source of the difference between these approaches can readily be seen if the cross-dependency equation is rewritten in a form which makes it equivalent to that used in the sole dependency method. In doing this, it is first necessary to recognise that the family income figure, here $50,000, is composed of the sum of the wife’s and husband’s incomes, that is, $30,000 + $20,000. Thus, the equation for the wife’s dependency in the cross-dependency approach, (equation (2)), may be rewritten:

0.70 x ($30,000 + $20,000) – $20,000 = $15,000 (3)

Furthermore, with rearrangement, equation (3) can be represented as:

(0.70 x $30,000) + (0.70 x $20,000 – $20,000) = $15,000 (4)

or as:

(0.70 x $30,000) – (0.30 x $20,000) = $15,000 (5)

That is, the difference between the sole dependency approach and the cross-dependency approach is that in the latter, the element (0.30 x $20,000), which is the portion of the wife’s income which had previously been devoted to the husband, is deducted from her loss of dependency.

c) A “revised” cross-dependency method

In this approach, the wife receives the husband’s total income net of the total amount devoted to his personal expenditures. Thus, as it has been assumed that the husband’s personal expenditures accounted for 30 percent of family income (and family income is $50,000), the wife would receive:

$30,000 – (0.30 x $50,000) = $15,000 (6)

Recognising, again, that the $50,000 family income figure in this equation is the sum of the husband’s and wife’s incomes, equation (6) can be rewritten:

$30,000 – (0.30 x ($30,000 + $20,000)) = $15,000 (7)

or:

$30,000 – (0.30 x $30,000) – (0.30 x $20,000) = $15,000 (8)

which, with simplification, becomes:

(0.70 x $30,000) – (0.30 x $20,000) = $15,000 (9)

Equation (9), however, can be seen to be identical to equation (5), the method for calculating a “traditional” cross-dependency. Hence, although the rationale for using equation (9) is different from that for equation (5), the two approaches yield the same result. It is for this reason that I used the term “revised” cross-dependency to describe the approach which was used to derive equation (9)

Three Types of Marriages

In this section, I discuss three types, or “styles,” of marriage and identify the appropriate dependency approach associated with each.

a) The idealised marriage. In what might be called an “idealised view of marriage”, the couple marries for love and shares all family income (approximately) equally. That 30 percent of family income is spent on items which benefit the husband alone implies that 30 percent of each of the husband’s and wife’s income is devoted to those expenditures. (And, conversely, 30 percent of each spouse’s income is devoted to items which benefit the wife alone.) The wife is assumed to spend 30 percent of her income on her husband because she loves him and, hence, derives pleasure from expenditures which benefit him.

In such a marriage, the pecuniary impact of the husband’s death is as follows: First, the wife has lost the 70 percent of the husband’s income (0.70 x $30,000 = $21,000) which he had spent on joint, family expenditures and on her personal consumption. Second, the wife now “saves” the 30 percent of her income, here $6,000 (= 0.30 x $20,000), which she had previously been spending on her husband’s personal consumption. However, it is not correct to say that she is “better off” by that $6,000. In the “idealised” marriage, her “gift” of $6,000 to her husband was voluntarily made because that use of her money gave her greater pleasure than any other use available to her. Thus, when the death of her husband “freed” her to spend the $6,000 on herself, she was not made better off. The “freeing” of the $6,000 forces her to purchase something – goods and services for herself – which she values less than the items she was purchasing before – goods and services for her husband.

A less emotion-laden example might help to explain this point. Assume that individual A has been leasing a car for $500 per month. The tortious intervention of individual B has destroyed the car and $1,500 of contents belonging to A. Although two months had remained on the lease, A has been excused from further payment (perhaps on the ground that the contract was frustrated). B admits that he owes $1,500 to A, to compensate him for the loss of his personal belongings, but argues that this should be offset in part by the $1,000 A has “saved” because he no longer has to make two months of lease payments. B’s argument is wrong. Although A now has $1,000 which he did not have before; he has been deprived of the use of a car, a use on which he had placed a value of at least $1,000. Instead of being made better off by the “gain” of that $1,000, he will actually be made worse off by the difference between the value of the car and the value of the “next best” set of goods and services which he can now purchase. Similarly, the wife who was previously devoting some of her income to her husband is not better off when she is prevented, by the tortious action of some third party, from spending that money. Rather, like the individual deprived of his car, she is worse off. Hence, in the idealised form of marriage, it is the sole dependency approach which is justified.

b) The marriage of convenience. The couple may not have married for reasons of love, but for reasons of financial gain. From a purely financial perspective, the marriage described above cost the wife $6,000 – the amount which she spent on items which benefitted her husband alone. In return, however, she received the benefit of the expenditures her husband made on her – 70 percent of his income, or $21,000. That is, she may be thought of as having “paid” $6,000 in order to receive $21,000. In such a marriage of convenience, the wife loses only the difference between these two figures – $15,000 – when her husband dies. (Note: the husband has also gained from this marriage, as he has “paid” 30 percent of his income, or $9,000, in order to obtain the benefit of 70 percent of his wife’s income, $14,000.)

In such a marriage, it is the “traditional” cross-dependency approach which is justified – subject to the following caveat: The 30 percent of the wife’s income which benefitted the husband alone must have been less than the 70 percent of the husband’s income which benefitted the wife, (and vice versa), otherwise the marriage would not have provided a financial gain to the wife. For example, if the wife’s income had been $50,000 and the husband’s $20,000, the wife would have spent (0.30 x $50,000 =) $15,000 on the husband in return for only (0.70 x $20,000 =) $14,000. Such an outcome would have been possible in an “idealised” marriage, but not in one which had been entered for financial gain.

c) A marital partnership. Although the couple may have married for love, they may have agreed to maintain separate bank accounts, with each spouse paying for those items which benefitted him/her alone. In this case, it is only that portion of the deceased’s income which was spent on joint household expenditures which the surviving spouse will have lost. In the example developed above, the husband was assumed to have earned $30,000 and the wife $20,000. Thirty percent of total family income, or (0.30 x $50,000 =) $15,000, was for the husband’s benefit alone. In the “marital partnership” model, the husband is assumed to have paid for all of the latter expenditures. What remained of his $30,000 income, after deduction of this figure, was the husband’s expenditure on items which benefitted the couple jointly. That amount is also $15,000 (= $30,000 – $15,000). It is the “revised” cross-dependency approach which would compensate the wife for the loss of this amount.

It will be noted that the loss of dependency calculated on this basis, $15,000, is identical to that calculated according to the “traditional” cross-dependency approach. This is not a coincidence. Mathematically, the two can be shown to be identical to one another. Hence, the use of the cross-dependency approach can be justified on the basis of either the “marriage of convenience” or the “marital partnership” model. It should be cautioned that both suffer from the reductio ad absurdum that individuals earning relatively high incomes will be found to be “better off” when their spouses are killed.

Conclusion

It is now seen that there is not a unique approach which can be applied to all marriages. Rather, one must consider the nature of the relationship which had been shared between the deceased and the plaintiff. Two types of evidence can be led: subjective and objective.

a) Subjective evidence. Subjective evidence concerns the nature of the personal relationship which had existed between the husband and wife. If evidence is led to indicate that the marriage in question had been based on love and mutual respect, a prima facie case would appear to have been made for use of the sole dependency approach. Only if it could be shown that the marriage was one of “convenience” would it be appropriate to employ the traditional cross-dependency approach.

b) Objective evidence. Objective evidence concerns the extent to which the couple had intermingled their incomes and paid for personal and household items jointly. Even when the court is reluctant to rule on the basis of the presence or absence of a “loving” relationship, use of the sole dependency approach can be justified on the pragmatic ground that many couples combine their incomes in a single pool, within which it is impossible to distinguish one individual’s contribution from the other’s. Hence, if 30 percent of the (family) income in this pool is spent on the husband, for example, it would not make sense to argue that 30 percent came entirely from his income. Rather, the more reasonable conclusion would have to be that 30 percent derived from his contributions to family income and 30 percent from his wife’s contributions – that is, that the sole dependency approach should be employed.

On the other hand, if the couple had carefully kept their accounts separate from one another, a strong presumption would appear to have been made for use of the “revised” cross-dependency approach – unless the individuals had markedly different incomes. (If the wife’s income was $10,000 per year and her husband’s $50,000, for example, it would be extremely unusual to find that the husband had spent 60 percent of “his” $50,000 income on items specific to himself; while only 60 percent of the wife’s $10,000 income had been spent on items specific to her.)

leaf

Christopher Bruce is the President of Economica and a Professor of Economics at the University of Calgary. He is also the author of Assessment of Personal Injury Damages (Butterworths, 2004).