by Kris Aksomitis
This article was originally published in the autumn 1998 issue of the Expert Witness.
The most reliable source of information about the incomes of specific occupations is the census. Unfortunately, census data are collected only once every five years — and income data are not published until three years after they are collected. (For example, income data from the 1995 census were not available until July of 1998.)
As a result, if census data are to be used, some method must be found for updating those data between the most recent census year and the year in which the information is required. For example, to use census income data in early 1998 (before the release of the 1995 census data), estimates of 1998 earnings had to be based on data from the 1990 census. This updating is achieved by increasing the relevant census figure by an estimate of the percentage increase in earnings between the most recent census year and the year in question.
The data series which is most often used to obtain this estimate is Statistics Canada’s Annual Estimates of Employment, Earnings and Hours (Cat. 72F0002XDE). This series reports estimates of average weekly earnings by
industry. Hence, as the desired figure is income by
occupation there is some concern that growth rates based on the Statistics Canada occupational earnings series will fail to provide an accurate estimate of the desired increase.
To my knowledge, no one has attempted to test whether industry growth rates provide an accurate estimate of occupational growth rates. That is the purpose of this article.
Here, I calculate the growth rates of incomes in various
occupations between the 1990 and 1995 censuses and compare those growth rates to estimates of those rates, which have been obtained from the annual growth rates of
industry earnings.
Methodology
The purpose of the article is to test the accuracy of using industry growth rates to predict average earnings for specific occupations. As such, the procedure uses the following steps:
- First, a number of occupations were selected as a basis of comparison. The selection process was fairly arbitrary, but an attempt was made to include occupations from a number of distinct industries.
- Second, data were collected for the chosen
occupations from the 1990 Census and the 1995 Census. These figures represent the actual annual average incomes for these occupations in the respective years. The ratio of the incomes in 1995 and 1990 were calculated for each occupation. - Third, data were collected on industry income growth rates. These figures were calculated from average weekly earnings for the specific industries in question, and were used as proxies for salary growth rates within those industries.
[Note that the calculated figures for both industry and occupation are simple percentages and not compound growth rates. For example, the calculated “all occupations” growth factor of 13% means that earnings increased 13% in total over the 5 years, or slightly less than 2.5% compounded annually. For each industry or occupation, the growth factor was calculated by dividing the value of 1995 earnings by the value of 1990 earnings.] - Fourth, the “actual” rate of growth of earnings for each occupation was compared to the growth rate of earnings from the industry that I believed to be most closely related to the occupation in question. In the table, below, I refer to these industry growth rates as “estimated” rates of growth as they represent our best estimates of the growth of occupational earnings.
- Finally, the actual occupational growth rates were compared with both the estimated growth rates and the average, “all-industry” growth rate.
Analysis
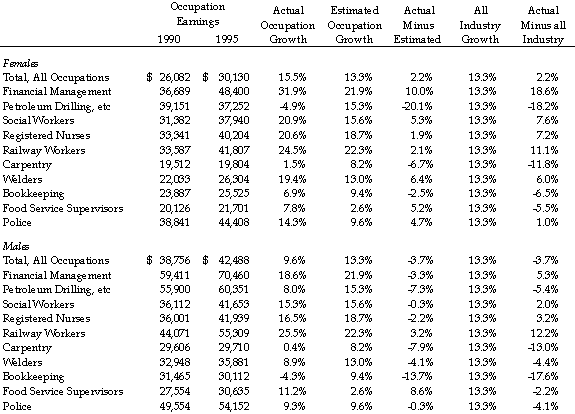
The table presents the results. A number of interesting observations can be drawn from the data. The first, and most important observation, is that the industry specific growth rates provide a better estimate than the overall average growth rate in all but five cases.
From this observation, it can be argued that, for the most part, the industry-specific estimated growth rates provide a better estimate of earnings growth than do the average growth rates for the entire economy. Of the occupations I examined, only for male food service supervisors did the average growth rate provide a significantly better estimate than did industry-specific growth.
A second observation is that the estimates provided by the industry specific growth factor is quite accurate in the majority of the cases. For example, in 12 of the 22 cases, the estimated earnings are within 5.1% of the actual earnings. This indicates that, in these cases, the annual compound growth rate predicted by the estimate is within 1% of the actual annual growth rate in earnings.
Some of the errors can be explained by the small sample size of the occupations. This would appear to be the case, for example, with respect to female petroleum drillers. In other cases, for example male bookkeepers, it may be that individuals were spread among so many industries that no estimate from a single industry could be expected to prove accurate.
[Interestingly male bookkeepers and female drillers were the only two occupations of those I’ve examined whose
earnings were lower in 1995 than in 1990. In every other case, actual earnings increased over the 5-year Census period and the earnings estimates by the model provided a reasonable estimate of actual earnings.]
A final observation from the data is that the correlation between actual and predicted earnings seems highest in occupations which are characterised by a high degree of unionization. For example, accurate estimates were obtained for police, social workers, registered nurses and railway workers.
Conclusions
Overall, it seems that industry-specific growth rates provide a reasonable estimation of occupational growth. In the majority of cases, the specific industry growth rate provided a better estimation of actual earnings growth than did the general economy growth rate. Further, in many cases the industry wage growth rate provided an excellent proxy for the specific occupational growth rate, especially in those occupations that were most highly unionized and clearly defined as part of that industry.
![]()